Preis Obligation Rendite Kupon – Obligation und Rendite und Kupon am Beispiel erklärt!

Zuletzt aktualisiert & geprüft: 06.11.2019

Gerade für Anfänger im Bereich der Anleihen und sonstigen Obligationen ist es schwierig zu erkennen, wie hoch die Rendite einer bestimmten Anleihe ist. In vielen Fällen wird die Kuponzahlung, also der ausgezahlte Zinssatz, mit der Rendite der jeweiligen Anleihe verwechselt. Tatsächlich ist die Rendite mit der Kuponzahlung nur in einer Konstellation identisch. Diese ist in der Realität jedoch nur selten anzutreffen, gerade wenn der Markt bestimmten Fluktuationen unterliegt. Der folgende Artikel soll die Komplexität der Anleihenrendite beleuchten und darstellen, in welchem Rahmen der Preis, die Rendite und die Kuponzahlung einer Anleihe zusammenhängen.
Der Preis einer Obligation kann von unterschiedlichen Faktoren abhängen. Wie genau das Verhältnis zwischen diesen einzelnen Faktoren ist, hängt in erster Linie jedoch davon ab, wie die Obligationen gehandelt werden. Grundsätzlich kommt es darauf an, ob die Obligation zu pari, unter pari oder über pari gehandelt wird. Pari ist ein Fachbegriff für den Nennwert einer Anleihe. Der Nennwert einer Anleihe ist festgelegt. Bei einer Nullkuponanleihe beispielsweise wird der Nennwert als Endauszahlung der Anleihe bezeichnen.

Wird eine Obligation unter Pari, also unter ihrem Nennwert gehandelt, ist die Rendite auf Verfall größer als die Couponzahlung. Als Rendite auf Verfall bezeichnet man die restliche Rendite auf die verbleibende Restlaufzeit der Anleihe.
Wird die Obligation über Pari gehandelt, so ist die Rendite auf Verfall kleiner als der Coupon
Wird die Rendite zu Pari gehandelt, so sind der Coupon und die Rendite identisch.

Jetzt zum Testsieger eToro!74% der Konten von Kleinanlegern verlieren Geld beim Handel mit CFDs bei diesem Anbieter. Sie sollten sich überlegen, ob Sie das hohe Risiko, Ihr Geld zu verlieren, eingehen können. Krypto-Investitionen werden von eToro (Europe) Ltd. angeboten und die Verwahrung wird von eToro Germany GmbH durchgeführt. Ihr Kapital ist gefährdet.

Wird eine Obligation übertragen, nachdem sie bereits emittiert wurde, so müssen abgelaufene Zinsen einkalkuliert werden, damit der vorherige Besitzer nicht auf die vorherigen, akkumulierten Zinsen verzichten muss. Diese machen einen Teil seiner Rendite aus.
Damit die Obligationen vergleichbar sind, müssen diese anhand der akkumulierten Zinsen gegenübergestellt werden. Dabei sind die unterschiedlichen Laufzeiten und die Couponzahlungen in unterschiedlichen Höhen zu beachten. Ein Käufer, der die Obligation von einem Inhaber übernehmen möchte, muss dem Verkäufer zusätzlich zum Preis in der Höhe der akkumulierten Zinsen auszahlen. Dem Verkäufer wird das Datum vorgelegt, an dem die Ausschüttung der Couponzahlung stattfindet. Dadurch erhält der Käufer die Zinszahlungen im Voraus. Er muss allerdings bis zur nächsten Ausschüttung warten, bis er seine vollständige Couponzahlung erhält.
Ein praktisches Beispiel soll dies verdeutlichen: Am 31.3.2015 notiert eine Obligation mit einem Zeitraum vom 01.01.2014 – 01.01.2019 mit einer Couponzahlung in Höhe von 8%. Der Nennwert beträgt 10.000 Euro, während die Obligation bei einem Preis von 98,15% notiert. Des jährliche Ausschüttungsdatum ist in der Mitte des Jahres, am 30.6.
Da ein Käufer die Obligation vom Inhaber am 31.03.2015 erwirbt, sind die akkumulierten Zinsen an diesem Datum an diesen auszuzahlen. Er selber muss bis zum 30.6 warten, um eine erste Zinszahlung zu erhalten. Bei einem Wert von 98,15% würde sich aus 10.000 Euro Nennwert folgende Rechnung für den Preis der Anleihe ergeben:
10.000 * 98,15% = 9.815 Euro + akkumulierte Zinsen: (360-61)/360*0,08*10.000= 664,44
Der Preis für die Anleihe ist somit 10.479,44 Euro. Dadurch, dass der Käufer bei Abnahme der Anleihe die akkumulierten Zinsen gezahlt hat, erhält er bei der nächsten Couponzahlung in der Mitte des Jahres den vollständigen Betrag von 800 Euro (10.000 Euro * 0,08= 800 Euro).
Die Art der Berechnung der akkumulierten Zinsen hängt davon ab, in welchem Land die Obligation ausgegeben wurde.
Die wichtigsten Länder, die Anleihen ausgeben und für die meisten Anleger aus dem deutschsprachigen Raum interessant sind, sind die USA, die Schweiz, Japan, England und Frankreich. Um einen Überblick über die unterschiedlichen Berechnungsarten zu erhalten, soll im Folgenden eine kurze Darstellung erfolgen.

Deutschland: Sowohl in der Schweiz, als auch in Deutschland werden die akkumulierten Zinsen mit einem fiktiven Zinsjahr mit 360 Tagen berechnet. Die 12 Monate sollen durchschnittlich 30 Tage haben. Die akkumulierten Zinsen ergeben sich daher aus der folgenden Formel = (30 * Anzahl Monate + Tage seit der letzten Couponzahlung) / 360 * Jährliche Couponzahlung) = (30 * M + D) / 360 * Cp

USA: Bei den Treasury Bonds wird auf eine genaue Anzahl von Tagen geachtet und mit einer halbjährlichen Verzinsung gerechnet. Daher werden die akkumulierten Zinsen so berechnet = genaue Anzahl der Tage seit letzter Auszahlung / genaue Anzahl zwischen den Coupons * (Cp / 2)

USA: Bei den US Domestic Bonds, welche etwa Unternehmensanleihen sein könnten, wird eine Formel, die der Deutschen ähnlich ist, benutzt. Dabei wird allerdings von einer halbjährlichen Verzinsung ausgegangen = (30 * M + D) / 360 * Cp/2

Japan/England: In Japan und in England wird auf eine Verwendung eines Geschäftsjahres mit 365 Tagen und eine genaue Abrechnung der Zinsen wertgelegt. Daher berechnen sich die akkumulierten Zinsen wie folgt = (aktuelle Tage seit letztem Coupon) / 365 * Cp/2

Frankreich: In Frankreich werden bei der Berechnung der akkumulierten Zinsen die genaue Anzahl der Tage seit der letzten Ausschüttung und die genaue Anzahl von Tagen zwischen den genauen Ausschüttungen berücksichtigt. Daher werden die akkumulierten Zinsen wie folgt berechnet: genaue Anzahl von Tagen seit letzter Zahlung / genaue Anzahl von Tagen zwischen den Zahlungen * Cp

Neben der Berechnung des Preises einer Obligation ist es von enormer Bedeutung die Rendite einer Obligation berechnen zu können. Dabei gibt es unterschiedliche Arten der Rendite einer Anleihe. Eine davon ist die aktuelle Rendite (Current Yield). Die Berechnung ist vergleichsweise einfach, da lediglich der jährliche, vertraglich vorgeschriebene Cash-Flow durch den Preis, zu dem die Anleihe am Markt notiert ist, dividiert werden muss: Rakt = C / Po ( C= Höhe des Cashflows, Po = Marktpreis). Generell verhält sich die aktuelle Rendite gegenteilig zum Kursverlauf des Preises der Anleihe. Eine steigende aktuelle Rendite ist stets mit fallenden Preisen verbunden, während eine fallende aktuelle Rendite mit einem fallenden Kursverlauf verbunden ist. Um jedoch verschiedene Anleihen zu vergleichen, ist die aktuelle Rendite kein angemessener Maßstab. So gibt es bei Nullkuponanleihen beispielsweise keine aktuelle Rendite, da diese während der Laufzeit keinen Coupon auszahlt. Eine Anleihe die jedoch unter ihrem Nominalwert gehandelt wird, weist in den meisten Fällen eine sinkende aktuelle Rendite auf.

Die Yield to Maturity hingegen ist die Rendite auf Verfall. Sie wird als Diskontsatz r bezeichnet und entspricht dem Wert der künftigen Cashflows aus einer Anleihe bis hin zum Ende der Laufzeit. Er stimmt ebenfalls mit dem aktuellen Marktwert der Anleihe überein:

(CFt= Cash Flow, der am Ende der Periode t fällig ist; T= Restlaufzeit der Anleihe)
In der Literatur wird der Yield to Maturity auch als der interne Zinssatz bezeichnet. Sie ist jedoch mit der Annahme zu berechnen, dass die Anleihe bis zum Ende der regulären Laufzeit gehalten wird. Oftmals wird sie mit der Gesamtrendite verwechselt.
Im Rahmen einer halbjährlichen Verzinsung sind die Zinssätze unterschiedlich zu berechnen. Was sich hierbei ändert, ist das sich die Anzahl der Perioden verdoppelt und die Zinszahlungen dementsprechend zwei mal jährlich stattfinden: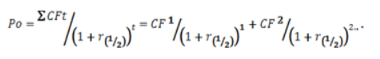

Der Cash Flow ist stets am Ende der Periode fällig. Zinstechnisch wird er mit dem halbjährlichen Zinssatz diskontiert. Außerdem muss die halbjährliche Rendite in eine jährliche Rendite transformiert werden. Hierbei ist wiederum die Art der Zinsberechnung der jeweiligen Länder zu berücksichtigen.
Am europäischen Markt gilt dabei die folgende Formel zur Berechnung der ganzjährigen Rendite: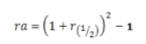

Am US-amerikanischen oder Englischen Markt gilt:

Bei US-Amerikanischen und englischen Markt wird der jährliche Zinssatz nicht verzinst, was die Rendite allgemein verringert.
Ein weitere Art der Renditeberechnung ist die zwischen zwei Zahlungsterminen. Diese Art der Berechnung ist vor allem dann wichtig, wenn ein Käufer die Anleihe von einem Inhaber erwirbt. Er muss dem Verkäufer die gesamten akkumulierten Zinsen bezahlen. Er selber erhält die Zinsen erst zum Zeitpunkt der nächsten Ausschüttung. Um den gesamten Wert der Anleihe zu erhalten, muss folglich der Preis plus die akkumulierten Zinsen berechnet werden: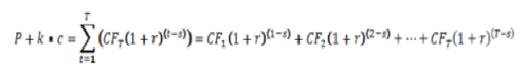

Auch hier muss die unterschiedliche Art der Anleihenberechnung einkalkuliert werden.

Nachdem bereits darauf eingegangen worden ist, wie der Preis einer Anleihe zustande kommt, wie die Renditen vergleichbar berechnet werden und wie die Anpassungen an die lokalen Märkte vorgenommen werden können, sollen im folgenden die Faktoren, die Auswirkungen auf die Rendite einer Anleihe haben, erklärt und dargelegt werden.
Der Zusammenhang zwischen dem Kupon und der Rendite wurde bereits angerissen und soll im folgenden wörtlich ausgedrückt werden. So muss zunächst zwischen einer Nominalverzinsung und einer effektiven Verzinsung eines Kapitals unterschieden werden. Die Verzinsung ist die Rendite der Anleihe, da der Kapitalgeber mit dem Zinssatz für die Überlassung seines Kapitals an den Emittenten vergütet wird. Die Nominalverzinsung beschreibt die Verzinsung, die vertraglich festgelegt wird. Diese kann entweder fix oder variabel sein. Insgesamt hängt die Höhe des Zinssatzes von der Bonität des Emittenten, den Sicherheiten, den aktuellen Marktbedingungen, dem Leitzinssatz und der Höhe der Rendite vergleichbarer Anleihen ab. Die Kuponzahlung erfolgt zu festgelegten Zeitpunkten innerhalb der Laufzeit. Dies könnte zum Beispiel am Ende des Jahres oder zwei Mal jährlich sein. Die Null-Kupon-Anleihe hingegen wird anders behandelt. Sie kann entweder als Zinssammler fungieren, sodass alle angesammelten Zinsen am Ende der Laufzeit ausgezahlt werden. Andernfalls kann sie als zu einem niedrigeren Wert ausgezahlt werden, sodass am Ende der Laufzeit der faire Nennwert bezahlt wird.
Die Nominalverzinsung ist jedoch kein Maß für die effektive Verzinsung der Anleihe. Die effektive Verzinsung setzt sich aus der nominalen Verzinsung und aus dem Kursgewinn/-verlust zusammen. Im Rahmen einer Transaktion der Rendite oder einer Berechnung der vorzeitigen Rendite werden die oben erwähnten Methoden in Frage kommen. Was oben jedoch noch nicht aufgeführt wurde, war die Berechnung der Rendite in Zusammenhang mit dem Anleihenkurs.
Grundsätzlich ist die Rendite von einem bestimmten Stichtag abhängig, an dem sie bewertet werden soll. Da während der Laufzeit der Anleihenkurs einer Rendite heftig schwanken kann, ist die Rendite einer Anleihe ebenfalls schwankend und daher stark an den Anleihenkurs geknüpft.
Generell fällt der Anleihenkurs tendenziell, wenn die wirtschaftlichen Rahmenbedingungen sich für den Emittenten nachhaltig verschlechtern. Diese können sowohl externer, also gesamtökonomischer Natur, oder interner, also betriebswirtschaftlicher Natur sein. Die Bonität des Emittenten wird daraufhin abgestuft werden, was zur Folge hat, dass sich das Rating und daraufhin der Preis der Anleihe verschlechtert. Bei einer positiven Entwicklung der genannten Faktoren wird sich die Bonität und somit das Rating und der Preis verbessern, was zur Folge hat, dass sich die Rendite der Anleihe insgesamt erhöht. Die Veränderung des Leitzinssatzes ist ein hervorragendes Beispiel für die Veränderung der Marktbedingungen und des direkten Einflusses auf die Rendite einer Anleihe.
Ein Investor muss sich also die Frage stellen, ob eine Anleihe mit einer hohen Rendite ein Anzeichen für ein unsicheres Investment sein könnte oder aber, ob es sich um ein hervorragendes Investment handelt. Die Antwort auf diese Frage kann jedoch nicht einfach gegeben werden. In der Regel gilt es, ähnliche Anleihen zu finden und deren Renditen zum Vergleich heranzuziehen. Liegen die Renditen einer Anleihe deutlich über dem Durchschnitt, beispielsweise einer Bundesanleihe, so ist diese wahrscheinlich in der Tat mit einem höheren Risiko verbunden. Ist der Emittent einer Anleihe sich sicher, dass er in der Lage sein wird, das geliehene Kapital zurückzuzahlen, so wird er in der Regel mit Leichtigkeit zahlungswillige Investoren finden. Dementsprechend wird er nicht dazu gedrängt, einen hohen Zinssatz zahlen zu müssen.

Ein weiterer wichtiger Faktor, der einen enormen Einfluss auf die Preisnotierung einer Anleihe hat, ist die Laufzeit. Diese bestimmt nämlich den Anleihenkurs und die Kursentwicklung in der Zukunft. Anleihen, die nur noch eine relativ kurze Restlaufzeit haben, sind besonders gegenüber geldpolitischen Änderungen der Zentralbank empfindlich. Gerade momentan ist dies ein besonders wichtiges Thema, da die Phase der rekordverdächtigen Niedrigzinsen kurz vor dem Ende stehen könnte. Die FED-Chefin Yellen hat angedeutet, bereits in diesem Jahr eine Erhöhung des Leitzinssatzes in den USA anzustreben. Wichtig für ihre Entscheidung ist das Erreichen eines bestimmten Inflationsniveaus. Wird von den Anlegern ein Anstieg der Inflation erwartet, so wird der Kurs der Anleihen mit einer langen Laufzeit steigen. Sollte die FED somit in der Zukunft sich für eine Anhebung der Leitzinsen entscheiden, wird dies vermutlich in einer enormen Erhöhung der Renditen von Anleiheninhabern münden. Als die Leitzinsen gesenkt wurden, haben Anleihen mit kurzfristigen Laufzeiten von einem Kursanstieg profitieren können.
Ebenfalls wichtig für die Rendite und somit für den Preis einer Anleihe ist die Aktienmarktvolatilität. Die Volatilität bedeutet in der Regel ein höheres Risiko, aber auch höhere Ertragschancen für Anleger. Grundsätzlich bedeutet der Crash des Aktienmarktes, dass die Anleihenkurse steigen. Ein Anstieg im Aktienmarkt bedeutet demgegenüber ein Abfall im Anleihenmarkt.