Bestimmungsgrößen der Yield-Kurve

Zuletzt aktualisiert & geprüft: 14.11.2019

Die Yield-Kurve zeigt Zinsentwicklungen, die sich auf den jeweiligen Finanzhandel auswirken und zukünftiges Handeln innerhalb des Finanzmarkts bestimmen. Die Yield-Kurve stellt grafisch das Verhältnis zwischen der Yield to Maturity und den Restlaufzeiten von Obligationen dar und kann auf verschiedene Arten dargestellt werden. Zur Bestimmung der Yield-Kurve dienen verschiedene Variablen. Die Bestimmung hilft bei der Sicherung von Renditen. Zudem existieren verschiedene Darstellungsformen, Bestimmungsmethoden, komplizierte Terminzinsstrukturen und Optimierungsverfahren der Yield-Kurve eine wichtige Rolle für die tägliche Datenanalyse der jeweiligen Zinssätze.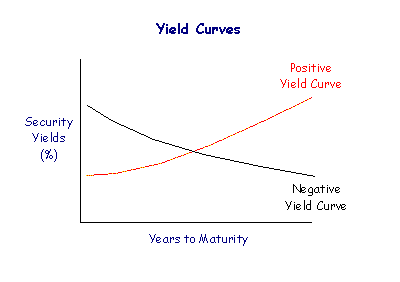

Jetzt zum Testsieger eToro!74% der Konten von Kleinanlegern verlieren Geld beim Handel mit CFDs bei diesem Anbieter. Sie sollten sich überlegen, ob Sie das hohe Risiko, Ihr Geld zu verlieren, eingehen können. Krypto-Investitionen werden von eToro (Europe) Ltd. angeboten und die Verwahrung wird von eToro Germany GmbH durchgeführt. Ihr Kapital ist gefährdet.

Inhaltsverzeichnis Anzeigen

Die verschiedenen Arten der Yield-Kurve

Eine normale Yield-Kurve liegt vor, wenn eine längere Laufzeit oder ein höheres Kreditrisiko einen höheren Yield bedingen. Zudem besteht die Möglichkeit einer inversen oder aber einen flachen Yield-Kurve, das geschieht jedoch nur selten. Der Yield einer kurzfristigen Obligation ist meistens niedriger als der Yield einer langfristigen Obligation. Die Yields der verschiedenen Obligationen bilden zusammen eine Yield-Kurve. Dies ist bei zahlreichen Entscheidungen von Bedeutung, beispielsweise hinsichtlich des Risikos und der Laufzeit. Je nach Einschätzung des Risikos wird eine bestimmte Rendite gefordert. In Ausnahmesituationen wie bei Marktängsten oder bei steigender Inflation ist es möglich, dass inverse Yield-Kurven entstehen. Die Zentralbank sorgt dann dafür, dass der Yield bei kurzfristigen Obligationen höher ist als der Yield langfristiger Obligationen. Die flache Yield-Kurve visualisiert ein Gleichgewicht zwischen den Renditen kurz- und langfristiger Obligationen. Der Darstellung der Yield-Kurve werden meistens Staatsobligationen zugrunde gelegt. Es existieren vier verschiedene Grundformen der Yield-Kurve:

die normale Yield-Kurve
die inverse Yield-Kurve
die flache Yield-Kurve
die Buckel-Kurve

Bei einer normalen Kurve steigen die Zinsen stetig. Die inverse Yield-Kurve entsteht, wenn Investoren den Yield in die Höhe treiben. Bei einer flachen Yield-Kurve bleibt die Yield to Maturity die ganze Zeit auf demselben Niveau. Die Buckelkurve steigt zunächst an und fällt dann ab. Deshalb kann sich der Anstieg einer Yield-Kurve möglicherweise zunächst auch als ein Risiko darstellen und die genaue Bestimmung der jeweiligen Kurven ist von großer Bedeutung, damit es nicht zu groben Missverständnissen kommt. Es ist beispielsweise möglich, dass eine Buckelkurve den Übergang von einer normalen in eine inverse Kurve darstellt.

Die Bestimmungsgrößen der Yield-Kurve

Die Yield-Kurve verdeutlicht auf grafische Weise die Beziehung zwischen der Yield to Maturity und den Restlaufzeiten. Die Yield-Kurve kann auf verschiedene Arten bestimmt werden. Zur Bestimmung dienen die folgenden Bestimmungsgrößen:

der reale Zinssatz
die Inflationsprämie
die Risikoprämie

Der reale Zinssatz ist der Betrag, den der Investor für seinen Verzicht auf den aktuellen Konsum erhält. Dieser Zinssatz gibt die Wertänderung eines Vermögens unter Berücksichtigung der Inflation an. Die Inflationsprämie bezeichnet die prognostizierte Inflation und kompensiert entstandene Kaufkraftverluste. Der nominale Zinssatz setzt sich aus der Addition des realen Zinssatzes, der erwarteten Inflationsprämie und der Risikoprämie zusammen:

realer Zinssatz + erwartete Inflationsprämie + Risikoprämie = nominaler Zinssatz

Häufig erhöhen Investoren die prognostizierte Inflationsprämie, denn dies erhöht zudem die Kaufkraft. Die Risikoprämie sichert den Investor gegen alle möglichen Risiken wie das Default-Risiko oder das Rückzahlungsrisiko ab. Auch das Bonitätsrating der Marktteilnehmer spielt für die Bestimmung der Yield-Kurve eine Rolle. Zunächst werden die Yield-Sätze und die Restlaufzeiten analysiert. Dadurch wird dann die Yield-Kurve bestimmt. Zudem gibt es Yield-Kurven für Obligationen mit verschiedenen Ratings. Es gilt dabei der bekannte Grundsatz, dass Zeit seinen Preis hat. Dies betrifft beispielsweise auch die Zinssätze in Verbindung mit den jeweiligen Restlaufzeiten. Die Bewertung und die Strategie von verzinslichen Wertpapieren werden stetig weiterentwickelt und Investoren beschäftigen sich mehr und mehr mit neuen wirtschaftlichen Instrumenten. Diese Instrumente ermöglichen dann optimale Strategien und exakte Bewertungen, um die Renditen zu sichern und Verluste zu verringern.

Darstellungsformen und Bestimmungsmethoden der Yield-Kurve

Jede Yield-Kurve lässt sich in ihrer Darstellung in eine andere Kurve umrechnen. Dabei kann beispielsweise zwischen einer zweidimensionalen oder einer dreidimensionalen Darstellung gewählt werden. Zur jeweiligen Darstellung dienen teilweise Daten aus anderen Yield-Kurven, wie beispielsweise die Renditen von Nullcouponanleihen mit verschiedenen Restlaufzeiten oder die Preise von Staatsanleihen. Weitere Bestimmungsgrößen, wie beispielsweise die Bonität des Schuldners, sollten konstant sein. Zudem orientiert sich die Yield-Kurve an den aktuellen Marktzinssätzen. Aus Swapsätzen werden mit Hilfe des sogenannten Bootstrapping die Zerocurve-Zinssätze und die Diskontfaktoren der Yield-Struktur bestimmt. Die Diskontfaktoren werden bei diesem Verfahren sukzessive bestimmt.

Bei der Bestimmung des Bid- oder Offerswapsatzes wird der Mittelwert herangezogen werden. Es existieren zudem zahlreiche Methoden, die Yield-Sätze am unteren Ende der Yield-Kurve zu bestimmen. Dazu werden beispielsweise die Yield-Sätze von Forward Rate Agreements getroffen. Die Yield-Struktur kann außerdem durch Forwardpreise auf Couponanleihen bestimmt werden und es werden statistische Verfahren für die Bestimmung der Yield-Kurve und der Yield-Struktur angewendet. Diese Verfahren werden in diskrete und stetige Statistikverfahren unterschieden. Zur Bestimmung einer Arbitragemöglichkeit werden die Terminsätze und die Diskontstrukturkurven analysiert.

Der Nutzen der Yield-Struktur

Yield-Kurven ermöglichen eine präzise Darstellung und Analyse der Erwartungen am Finanzmarkt und dienen einem gezielten weltweiten Vergleich der Schutzergebnisse. Darüber hinaus können aus der Struktur der Zinssätze (implizite) Terminzinssätze errechnet werden. Im Folgenden wird die Methode zur Bestimmung der Yield-Kurve näher verdeutlicht.

Die Yield-Kurve zeigt den Zusammenhang zwischen den Zinssätzen und Laufzeiten von Nullkuponanleihen ohne Kreditausfallrisiko. Von geldpolitischem Interesse ist sie in erster Linie als Indikator für die am Markt vorherrschenden Zins- und Inflationserwartungen. Ein Ansteig einer Yield-Kurve kann Auskunft über erwartete Veränderungen der Zinssätze oder der Inflationsraten geben. In den Veröffentlichungen der Deutschen Bundesbank wurde sie bislang näherungsweise durch eine Renditenstrukturkurve abgebildet. An die Stelle dieses Ansatzes tritt künftig eine direkte Bestimmung der Yield-Kurve. Diese Darstellung wird auf den weltweiten Finanzmärkten mehr und mehr verwendet. Die Analyse und die Entscheidung über den funktionalen Zusammenhang zwischen Zinssätzen und Laufzeiten werden dabei vom Verwendungszweck der Schätzungen bestimmt. Die Daten werden genau beobachtet und beschrieben. Die von Nelson und Siegel entwickelte und von Svensson erweiterte Methode ist eine gute Lösung für eine optimale Analyse der Daten. Der Zinssatz wird bei dieser Berechnung als die Summe aus einer Konstanten und verschiedenen Exponentialtermen und als Funktion von insgesamt sechs Parametern definiert. Die funktionale Form nach Nelson und Siegel enthält nicht den letzten Term. Die Erweiterung dieser wirtschaftlichen Methode durch Svensson ermöglicht einen weiteren Wendepunkt der geschätzten Kurve. In den Bundesbank-Publikationen wird meistens auf die Spezifikation gemäß Svensson zurückgegriffen, zumal dies eine bessere internationale Vergleichbarkeit der Ergebnisse gewährleistet. Der parametrische Ansatz mit Exponentialtermen ist laut Deutscher Bank in seiner ursprünglichen Formulierung durch Nelson und Siegel und in der Erweiterung durch Svensson ausreichend flexibel, um die am Markt beobachteten Datenkonstellationen wiederzugeben. Diese Datenkonstellationen visualisieren sich beispielsweise in folgenden Darstellungsarten der Yield-Kurve:

monoton steigende Yield-Kurve
monoton fallende Yield-Kurve
u-förmige Yield-Kurve
invertiert-u-förmige Yield-Kurve
S-förmige Yield-Kurve

Optimierungsverfahren der Yield-Kurve

Bundeswertpapiere beispielsweise werden täglich geschätzt. Den Schätzungen liegen die Kurse von Bundesanleihen, Bundesobligationen und Bundesschatzanweisungen mit Laufzeiten von mindestens drei Monaten zugrunde. Die Parameter werden mit Hilfe eines nichtlinearen Optimierungsverfahrens bestimmt. Als Optimierungskriterium wird in der Regel die Minimierung der quadrierten Abweichungen der geschätzten von den beobachteten Renditen verwendet. Renditenirrtümer werden minimiert: Es handelt sich bei den Schätzungen um Zinsschätzungen. Darüber hinaus existieren implizite Terminzinsen, die bei den Analysen berücksichtigt werden. Implizite Terminsätze sind nicht direkt beobachtbar.

Komplizierte Terminzinsstruktur

Eine Geldanlage liefert für einen bestimmten Zeitraum denselben erwarteten Ertrag. Demzufolge entspricht der einjährige (implizite) Terminzinssatz dem für den gleichen Zeitpunkt erwarteten einjährigen (Kassa-) Zinssatz. Die Yield-Kurve kann dann eine Steigerug anzeigen und wird als Differenz der Zinssätze für verschiedene Laufzeiten bestimmt. Dadurch gibt die Yield-Kurve Aufschlüsse über die erwarteten durchschnittlichen Veränderungen der kurzfristigen Zinssätze während des entsprechenden Zeitraumes. Der Verlauf der Terminzinsstrukturkurve zeigt dagegen unmittelbar die erwartete künftige Entwicklung der (Kassa-) Zinssätze. Dies ermöglicht eine bessere Trennung der Erwartungen über die kurze, mittlere und lange Frist als dies im Fall der Yield-Kurve möglich ist. Diesbezüglich gelten jedoch Einwände gegen eine Interpretation der Yield-Kurve im Sinne der Erwartungstheorie. Auch für die Terminzinsstrukturkurve werden diese Einwände diskutiert: Aufgrund zeitvariabler Risiko- und Terminprämien, die implizite Terminzinsen beeinflussen können. Von einer vorschnellen Bewertung und Interpretation der Terminzinsstruktur wird unter Wirtschaftsforschern auf dringlichste Weise abgeraten. Eine direkte Bestimmung von Yield-Kurven ermöglicht in jedem Fall, die Struktur der Terminzinssätze zu bestimmen. Dies ist für die geldpolitische Analyse sehr nützlich und bietet bietet eine optimale Trennung der Erwartungen über verschiedene Fristen, die in der Yield-Struktur enthaltenen sind. Die folgenden Merkmale charakterisieren die Yield-Kurve und die Terminzins-Kurve:

positiv steigende Kurven-Verläufe

monotoner Anstieg oder monotones Sinken der Yield-Kurve
starke Zinsschwankungen bei kürzeren Terminzinssätze, höhere Maximalwerte, niedrige Minimalwerte als langfristige Zins- und Terminsätze

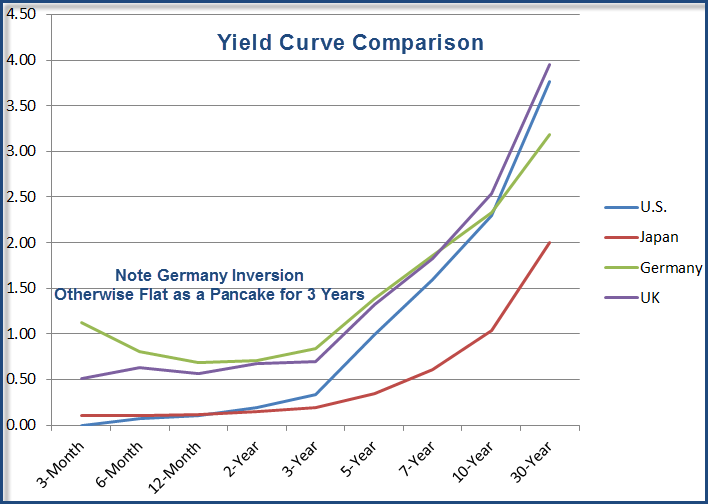
Normale Yield-Kurven gibt es sehr häufig, flache und inverse Kurven existieren selten. Gewöhnlicherweise verlaufen die Zins- und Terminzinsstrukturkurve monoton (positiv oder negativ). U-formige und S-förmige Kurvenverläufe treten äußerst selten und nur über relativ kurze Zeiträume auf. Änderungen der Kurvensteigung werden beispielsweise durch die Bewegung von kurzfristigen Zinssätzen beeinflusst. Die Yield-Kurve und die Terminzinsstrukturkurve stellen zu jedem Zeitpunkt dieselben Informationen bezüglich der Zinserwartungen auf unterschiedliche Weise dar. Die Zinssätze sind dabei ein Maß für den Kaufertrag zukünftiger Zahlungsströme, die zum Gegenwartswert erworben werden. Statistiken dienen einem präzisen Vergleich verschiedener Yield-Kurven. Yield-Kurven sind Momentaufnahmen, die sich zu jeder Zeit verändern können. Deshalb werden die Datensätze der Yield-Kurven stetig analysiert. Durchschnittliche Yield- und Terminzins-Kurven können auch zur Orientierung oder als Referenzwerte dienen, um weitere Kurven miteinander zu vergleichen und durch den Vergleich von vor kurzem vergangenen Ergebnissen und deren kurzfristige Entwicklung, Aufschlüsse über eine mögliche zukünftige Entwicklung bestimmter Yield-Kurven zu erhalten. Auch der Zeitpunkt, an dem der Durchschnitt gebildet wurde, ist bei dieser Art der Analyse sehr wichtig. Die Yield-Kurve zeigt Zinsentwicklungen, stellt grafisch das Verhältnis zwischen der Yield to Maturity und den Restlaufzeiten von Obligationen dar und kann auf verschiedene Arten dargestellt werden.

Weitere Faktoren der Bestimmung der Yield-Kurve

Zur Bestimmung der Yield-Kurve dienen verschiedene Variablen. Die Bestimmung hilft zudem bei der Sicherung von Renditen. Während des Handels auf dem Finanzmarkt spielen in der heutigen Zeit neben einem Mehrwert und einem Wachstum zahlreiche weitere Faktoren für Wirtschaftsteilnehmer eine immer größere Rolle: Weltweite Entwicklungen beeinflussen auch die Werte der Industriestaaten. Dabei ist es wichtig, Schulden direkt zu begleichen, weil die Zukunft irgendwann zur Gegenwart wird und die Schulden dann auf den jeweiligen Geschäftsteilnehmer zurückfallen. Deshalb ist es zudem nützlich mögliche Prämien zu nutzen, die Risiken abzuwägen und so viele Daten wie möglich in die Berechnungen einzubeziehen, die dann stetig wieder aktualisiert werden. Verschiedene Variablen und teilweise komplizierte Formeln dienen dabei der genauen Bestimmung. Für eine genaue Bestimmung müssen zudem immer wieder mögliche, neue Faktoren in Betracht gezogen werden. Zudem ist der aktuelle Zeitpunkt, jeder Moment, von großer Bedeutung, weil in jedem Moment ein neuer Bezug zum Finanzmarkt hergestellt werden kann. Diese Aktualisierungen dienen der genauen Schätzung des Finanzflusses, denn Marktteilnehmer möchten in der Regel Risiken vermeiden und nicht aus Euphorie handeln. Der Finanzmarkt erfordert zudem schnelle Reaktionen und flexibles Handeln: In einem solchen Moment ist es von Vorteil, wenn man Kenntnis von verschiedenen wissenschaftlichen Methoden in der Wirtschaft und von den verschiedenen Handlungsmöglichkeiten in den spezifischen Momenten hat. Dazu wird zudem stets grundsätzlich beachtet, dass die Geschäfte des Finanzmarkts mit zahlreichen Kosten verbunden sind. Die Rendite ist in jedem Jahr von Schwankungen betroffen. Das Wissen über die Bestimmungsgrößen der Yield-Kurve dient als Grundlage für die Analyse der zur Verfügung stehenden Daten.

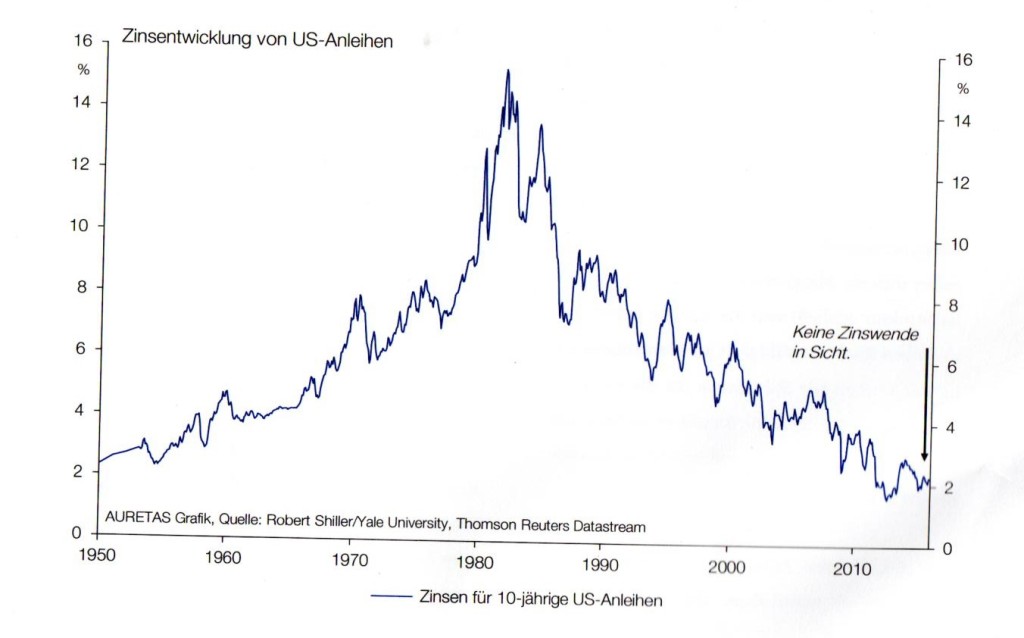
Die Bedeutung von Restlaufzeiten und Fälligkeitsdaten

Auch auf die Restlaufzeiten wird ein besonderes Augenmerk gelegt: Die Yield-Kurve zeigt das grafische Verhältnis zwischen der Yield to Maturity und den Restlaufzeiten von Obligationen. Dies betrifft die jeweiligen Fristen, Termine und Fälligkeitsdaten. Es ist deshalb für Marktteilnehmer sehr nützlich, sich spezielle Terminkalender anzulegen, um sicher keinen Termin zu versäumen, denn zum Ende der Laufzeit müssen Zahlungen getilgt werden. Dabei wird stets die Frage gestellt, wie sich die Zinsen analog zur der Zeit verhalten und an aktuelle Gegebenheiten anpassen. Bei einer optimalen Bestimmung der Yield-Kurve werden auch diese Daten einbezogen. Auch die Fälligkeitsdaten und die Bestimmungsgrößen der Yield-Kurve werden weiter differenziert und die Formeln für die Berechnungen und die Umrechnungen werden stetig weiterentwickelt. Darüber hinaus spielen auch rechtliche Grundlagen, Folgen und Veränderungen eine wichtige Rolle, beispielsweise für Anleger. Eine Yield-Kurve kann also auch in Bezug auf die Restlaufzeiten zahlreiche nützliche Informationen liefern, sodass weitere, erfolgreiche Geschäfte stattfinden können. Jeder Begriff hängt innerhalb des Finanzmarkts mit vielen weiteren Begriffen zusammen und wird damit zusammenhängend betrachtet, auch was beispielsweise sinnstiftende, weltweite Investitionen betrifft. Ein Finanzgeschäft ist ein Schuldverhältnis, das vor allem rechtlichen Grundlagen unterliegt, die im Zusammenhang mit der Börse festgelegt und zu einem Großteil weiterentwickelt werden.