Yield Worst Renditemessung – Die beeinflussenden Faktoren und Anwendung im Detail!

Das Verhältnis der Yield to Worst und dem Ausfallrisiko zeigt sich in folgender Formel:

Yield to Worst = 100 – Ausfallrisiko

Hierdurch wird ausgedrückt wie wahrscheinlich es ist die Yield to Worst zu erreichen. Hierbei gilt, dass bei einem Anstieg der Rendite das Erzielen dieser erschwert wird und im Gegenzug das Ausfallrisiko steigt. Grund dafür ist, dass eine hohe Rendite mit einem deutlich steigenden Risiko verbunden ist. Dieses Risiko wird durch die Möglichkeit gezeigt, dass die Rendite nicht dem erwarteten Wert entspricht.

Bedeutung für das Portfolio

Da es für den Investor meist nicht möglich ist zu wissen zu welchem Zeitpunkt dieser liquide Mittel benötigt, ist es zu empfehlen einen prozentualen Anteil an dem Vermögen zu einer Anlage zu verwenden, die ein geringes Risiko an Kursschwankungen besitzt. Eine Diversifikation im Portfolio ist demnach unabdingbar. Legt ein Investor zum Beispiel lediglich in Wertpapiere an, besteht meist ein großes Risiko bei einem kurzfristigen liquiden Engpass nicht auf das Anlagevermögen zurückgreifen zu können. Ziel bei der Konzipierung eines Portfolios ist es demnach dieses individuell auf den Anleger abgestimmt zu gestalten. Nachdem ein Portfolio mit Anlagen zu unterschiedlichen Laufzeiten angelegt worden ist, wird dem Investor ein dauerhaftes Investieren und dem Aspekt der Liquidität ermöglicht. Dies bedeutet, dass ein nicht planmäßiger Verkauf von Anlagen zu keiner Zeit angestrebt werden muss. Auch bei eventuellen Kursschwankungen ist der Investor bestmöglich abgesichert.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die Yield to Worst und ihre beeinflussenden Faktoren

Bei der Betrachtung der Yield to Worst wird diese von unterschiedlichen Faktoren definiert. Zu diesen zählen:

– die Prämie des Risikos

– die Opportunity Costs

– der Ausgleich der Inflation

– die Prämie der Liquidität

Der Zusammenhang zwischen der Prämie des Risikos und der Yield to Worst liegt darin, dass diese steigt, wenn das Risiko einer Anlage sich erhöht. Die Prämie der Liquidität wird in Abhängigkeit von der Laufzeit und der getätigten Investition ermittelt. Auch die gewählte Anlage hat Einfluss auf die Prämie der Liquidität. Die Opportunity Costs sind ebenso ein elementarer Faktor zu Definition der Yield to Worst, da diese als Basis für die Mindestrendite genutzt werden. Zudem ist die mögliche Inflation in die Errechnung der Yield to Worst zu integrieren.

Die Rendite und deren Standardabweichung

Mithilfe der Erstellung eines Portfolios kann eine geschätzte Entwicklung bestimmt werden. Da es sich bei der Bestimmung einer Entwicklung lediglich um eine Schätzung handelt, wird das Resultat der Analyse von dem in Zukunft erzielten Wert abweichen. Hierbei kann es sich um größere oder kleinere Abweichungen handeln. Generell geht eine größere Abweichung mit einem steigenden Risiko einher. Damit dieses Risiko identifiziert werden kann, wird folgende Formel genutzt:

Risiko = SD (R_p)

Liegt das Ergebnis dieser Rechnung bei beispielsweise 40 Prozent, ist die Wahrscheinlichkeit der Standardabweichung einer Rendite höher als im Vergleich bei einer Abweichung von 20 Prozent. In der Regel unterliegen zudem die Rentenportfolios geringeren Standardabweichungen als beispielsweise jene von Aktien. Eng mit der Standardabweichung verknüpft gilt die Prämie des Risikos. Häufig wird das Risiko deshalb der Standardabweichung gleichgesetzt.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die Streuung der Rendite und deren Kritik

Das Gleichsetzen des Begriffs der Standardabweichung und der Rendite stoßen auf Kritik, da die Streuung der Rendite auch jene in den oberen Bereich möglich ist, was zu einer positiven Entwicklung der Rendite führen würde. Somit wären die Möglichkeiten des Investors und dessen Risiken einander entsprechend. Da die Standardabweichung sich aus der Wurzel des Werts der Varianz ergibt, ist es von keiner Bedeutung, ob die abweichenden Werte positiv oder negativ sind.

Wird die positive mit der negativen Standardabweichung vom Erwartungswert verglichen zeigt sich, dass die negative Abweichung für den Investor einen größeren negativen Effekt hat, als die positive Abweichung einen Vorteil aufweist. Dies hat zur Folge, dass ein Schwanken der Rendite im positiven Bereich mit einem geringen Vorteil behaftet ist, während die Renditeschwankungen im negativen Bereich größere Folgen haben können. Hierbei gilt, dass stärkere Schwankungen die Gesamtheit der entstehenden Nach- und Vorteile verstärken.

Die Rendite und die Bedeutung der Varianz

Damit das Risiko von einem Portfolio definiert werden kann, müssen alle hierzu benötigten Kennzahlen betrachtet werden. Dies bedeutet, dass das Abweichen einer Rendite des Portfolios des Anlegers eine Betrachtung der wichtigsten Parameter inkludiert. Bei der Multiplikation einer Zufallsgröße Y mit einer Zahl b ergibt sich eine neue Zufallsgröße. Die Varianz sowie der Erfahrungswert dieser sind wie folgt zu berechnen:

E [b*Y] = b * E [Y]
Var [bY] = b² * Var [Y]
Aus diesen Formeln ist ersichtlich, dass bei einer Normalverteilung von Y diese auch für b * Y gilt. Plant der Anleger ein Vermögen V₀ heute mit einer Rendite R unter Normalverteilung anzulegen, dann ist innerhalb eines Jahres das Resultat.

V₁ = V₀ * (1 + R) ebenso normalverteilt. Hierbei ist b = V₀ und Y = (1 + R). Diese Berechnung zeigt, dass es für den Investor unwesentlich ist, ob dieser die Rendite oder das Ergebnis des Portfolios betrachtet. Bei einer normalverteilten Rendite wird ebenso das Ergebnis normalverteilt sein. Zusätzlich sind die Konstanten immer im gleichen Verhältnis zueinander. Als Schlussfolgerung aus dieser Rechnung lässt sich ableiten, dass die Verteilung der Wahrscheinlichkeit einer Rendite Aufschluss über das Ergebnis einer Anlage liefert.

Bei der Berücksichtigung einer weiteren Zufallsgröße mit dem Namen Z und einer Zahl c ergibt sich die Zufallsgröße c * Z. Diese wird zur Zufallsgröße b * Y hinzugezählt. Das hierbei entstehende Ergebnis spiegelt eine weitere Zufallsgröße wider. Diese ist

c * Z + b * Y. Deshalb gilt folgendes:

E [c * Z + b * Y] = b * E[Y] + c * E [Z]
Var [c * Z + b * Y] = b² * Var [Y] + c² * Var [Z] + 2 * b * c * Cov [Y;Z]

Ebenso wie in der vorigen Annahme gilt auch hier, dass wenn Z und Y eine Normalverteilung besitzen appliziert dies auch auf c * Z + b * Y. In der Theorie des Portfolios ist diese Annahme essenziell. Die Rendite des Portfolios ergibt sich somit aus der gewichteten Gesamtheit der Renditen jeder betreffenden Anlage, welche innerhalb eines Portfolios befindlich ist. Bei der Normalverteilung von Renditen der jeweiligen Anlagen trifft dies somit auch auf das gesamte Portfolio zu.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die Wahrscheinlichkeit des Ausfalls und die Yield to Worst

Das Risiko eines Ausfalls ist dann definiert, wenn der Investor die erwartete Rendite dazu benötigt ein Erfordernis erfüllen zu müssen. Im privaten Lebensbereich kann dies die Aufrechterhaltung eines gewissen Standards sein, während es für Unternehmen wichtig ist eine offerierte minimale Verzinsung zu erfüllen.

Das Risiko eines Ausfalls ist besonders von der Betrachtungsdauer der Anlage abhängig. Nach dem Ablauf der Laufzeit einer Anlage kann der Investor erkennen, ob die Yield to Worst erreicht wurde oder nicht. Auch innerhalb des Anlagezeitraums kann durch das Definieren der Durchschnittsrendite ersehen werden, ob die Yield to Worst erreicht wurde. Die durchschnittliche Ermittlung der Rendite ist jedoch von der Laufzeit der Anlage abhängig. Wird die durchschnittliche Rendite betrachtet zeigt sich, dass die Möglichkeit mindestens die Yield to Worst zu erreichen erhöht wird, wenn die Laufzeit als lang bezeichnet werden kann.

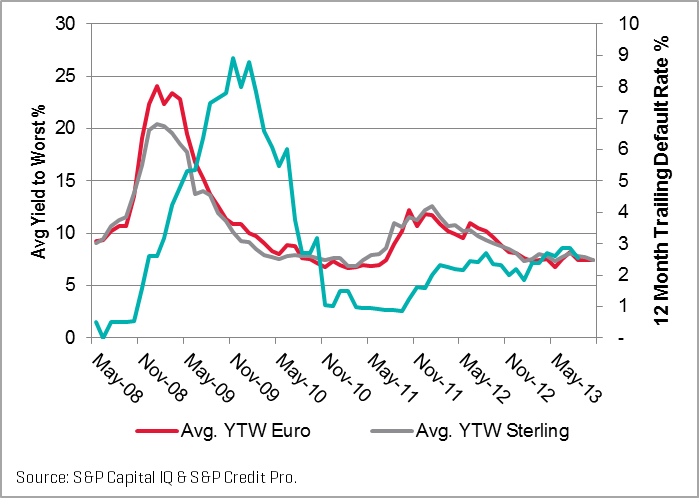
Die Yield to Worst und die unterschiedlichen Erwartungen an diese

Bei der Betrachtung des Yield to Worst im Rahmen der Messung der Rendite ist es wichtig, dass die Absicht des Investors analysiert wird. Ist der Investierende dazu verpflichtet aus der Rendite einer Anlage ein Geschäft erfüllen zu müssen, kann dies dazu führen, dass es zu einem größeren Nachteil für diese Person kommt, weshalb bei der Wahl einer Anlage auf das Abzielen des Investors geachtet werden sollte.

Hierbei kann das Ziel einer Anlage fix sein, damit nachfolgend die Verwendung der Rendite eingeplant ist. Hierdurch kann analysiert werden, wann mindestens eine Yield to Worst erwartet wird sowie welche Anlageformen in Betracht gezogen werden können. Ist das Ziel einer Anlage das zur Verfügung stehende Kapital zu vermehren, kann die Investition und deren Risiko hierauf abgestimmt werden. Die Folge hieraus ist, dass es keinen limitierten Zeitrahmen gibt, in welchem eine Yield to Worst erzielt werden muss.

Da es eine Vielzahl an Investoren gibt, welche demnach nicht das gesamte Vermögen zu einem definierten Zeitpunkt benötigen, kann dieser Betrag in einem angemessenen Verhältnis von Rendite und Risiko angelegt werden. Hierbei wird die Standardabweichung der Rendite eines Portfolios als Risiko genutzt.

Wird die erwartete Rendite mit der Standardabweichung betrachtet, kann die Wahrscheinlichkeit ermittelt werden, dass eine gewählte Rendite einer definierten Rendite entspricht, dieser unterliegt oder höher als diese ist. Hierbei wird angenommen, dass die normalverteilte Rendite kleiner oder gleich der gewünschten Rendite ist, wenn die um den Return subtrahierte Rendite kleiner oder gleich der gewünschten Rendite unter Abzug des Returns ist. Hierbei gilt:

R = Rendite

G = gewünschte Rendite

σ = Standardabweichung

µ = Return

Dies bedeutet, dass R – µ < G – µ wenn (R – µ)/σ < (G – µ)/σ. Da (R – µ)/σ eine Standardabweichung von eins sowie einen Erwartungswert von null besitzt gilt, dass diese entweder einen Wert von (G – µ)/σ oder einen niedrigeren Wert erreichen muss. Hierfür besteht die Wahrscheinlichkeit von N((G – µ)/σ). Dabei wird gezeigt, dass das Risiko ebenso vom Return abhängt. Zielt ein Investor darauf ab das eingesetzte Kapital zu erhalten, haben die Aktien ein ebenso hohes Risiko wie Anleihen. Bei dem Wunsch eine hohe Rendite anzustreben besitzen Aktien ein niedrigeres Risiko als Anleihen. Zudem ist es empfehlenswert im Rahmen der Erstellung eines Portfolios auf die Diversifikation der Anlagen zu achten, weshalb ein Investieren in Anleihen und Aktien sich positiv auf das zu erwartende Risiko auswirkt.

Die niedrigste Wahrscheinlichkeit eines Ausfalls – die Yield to Worst

Durch das Berücksichtigen der Mindestrendite sowie der gewünschten Rendite kann das Portfolio bestimmt werden, welches die niedrigste Wahrscheinlichkeit eines Ausfalls hat. Zudem wird die erwartete Rendite in diese Rechnung mit einkalkuliert. Auf dieser Basis gilt für Portfolios, dass Pr { R_p< G} verringert werden sollte. Dies bedeutet, dass N((G – µ_p)/σ_p) ebenso verringert werden muss. Aufgrund der Tatsache, dass N stetig ist, bedeutet dies, dass (G – µ_p)/σ_p verkleinert werden muss. Eine weitere Möglichkeit wäre, dass (µ_p – G)/σ_p erhöht werden kann. Ist die gewünschte Rendite hierbei dem Zinssatz entsprechend, zeigt dies die Performance der Anlage.

Mithilfe dieses Prinzips der Sicherheit kann ein Portfolio aufgebaut oder modifiziert werden. Bei der Anlage in Aktien zeigt sich, dass diese eine nahezu identische Performance haben wie beispielsweise Anlagen. Jedoch ist der Return bei Aktien höher, was durch das gesteigerte Risiko einer Standardabweichung ausgeglichen wird. Bei einer geringen Investition unter dem Umstand von gewünschten Renditen im niedrigeren Bereich liegt der Vorteil bei einer Anleihe, während eine Aktie zu einer gesteigerten gewünschten Rendite führen kann.

Eine weitere Möglichkeit die Yield to Worst im Portfolio zu berücksichtigen ist es diese mit einem möglichst hohen Wert zu versehen. Hierdurch wird jenes Portfolio gewählt, welches die höchste gewünschte Rendite aufweist. Das Risiko des Portfolios ist somit von der Zusammensetzung dieses abhängig. Die zu akzeptierende Wahrscheinlichkeit des Ausfalls wird unter der Berücksichtigung der Yield to Worst im Ansatz des Value-at-Risks betrachtet. Der einzige Unterschied besteht darin, dass bei der Betrachtung des Value-at-Risk der minimale Wert nicht als Rendite bezeichnet wird, sonder als monetärer Betrag.

Außerdem besteht die Option eine weitere Variante der Betrachtung in die Überlegungen miteinzubeziehen. Hierbei ist es wichtig, dass die Yield to Worst, die gewünschte Rendite sowie die Wahrscheinlichkeit des Ausfalls berücksichtigt wird. Beachtet werden sollte jedoch, dass die getroffene Auswahl nicht zu strikt erfolgt und es nachfolgend nicht zu einer Situation führt, dass kein Portfolio mehr infrage kommt. Im Anschluss an die Auswertung der Kennzahlen wird das Portfolio mit der besten Erwartung an Rendite gewählt.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die Problematik des Yield Managements – Yield to Worst

Nachdem die Bestimmung der Yield to Worst erfolgt ist, kann jedoch nicht von diesem Wert als fixem Wert gesprochen werden, da die Yield to Worst von vielen Faktoren abhängig ist, welche sich verändern können. Nimmt die Yield Kurve beispielsweise eine niedrigere Rendite von drei Prozent über eine Dauer von zwei Jahren an, kann dies für den Anleger vorteilhafter sein als eine Rendite von vier Prozent über sechs Jahre. Zudem gibt es für den Investor keine Garantie, dass der aktuelle Cashflow der angenommenen Laufzeit entspricht. Deshalb kann es von Vorteil sein den Yield Spread zu betrachten. Dieser hat den Vorteil, dass die Unsicherheit des Cashflows einer kündbaren Anleihe wegfällt.