Aktueller Wert des Geldes im Hinblick auf die Erschwernisse bei der Bewertung

Ein Notgroschen kann bekanntlich ein Versprechen sein, das nicht eingelöst werden kann. Beim Zusammenbruch eines Finanzsystems, wenn ein Not-Geld, ein Versprechen oder eine Verpflichtung nicht eingelöst werden können, wird klar, dass Geld nicht arbeitet. Durch mathematische Berechnungen können Aussagen getroffen werden, die eine Kalkulation von Ereignissen in der Zukunft ermöglichen, die sich beispielsweise häufig oder aufgrund verschiedener zugrunde liegender Daten ergeben. Auf einer Zeit-Skala steht dabei die Zukunft mit der Gegenwart in Verbindung. Auch unsichtbare Faktoren werden zudem in Berechnungen und Grafiken einbezogen. Die zukünftigen Werte sind dabei das Ergebnis der aktuellen Werte. Dennoch unterscheiden sich die Zahlungsströme, Zinssätze und der Wert des Geldes in der Gegenwart von Werten und Beträgen in der Zukunft.

Den aktuellen Wert des Geldes zu bestimmen, stellt sich in Bezug auf Werte in der Zukunft als Schwierigkeit dar: Es existieren beispielsweise verschiedene Zinssätze und Zahlungsströme können unvorhergesehen variieren. Für das nachhaltige Bestehen auf dem Finanzmarkt wird häufig der zukünftige Wert des Geldes berechnet und täglich müssen genaue Zukunftsprognosen getroffen werden. Auch der aktuelle Wert des Geldes kann berechnet werden. Dies dient dazu, herauszufinden, wie viel man in der Gegenwart sinnvoller Weise investieren sollte, um einen gewissen Betrag in der Zukunft zu erhalten. Es wird also auf den gegenwärtigen Wert des Geldes referiert. Der Gegenwartswert PV des Betrages P0 wird dann bezüglich des zukünftig zu erwarteten Zinssatzes r und einer Anzahl n bestimmter Perioden errechnet. Dadurch soll herausgefunden werden, welcher Betrag investiert werden muss, um in der Zukunft einen bestimmten Wert Pn zu erhalten. Für diese Berechnung wird in der Regel folgende Grundformel verwendet:

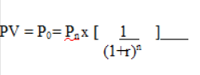
Die Ziffer 1 in diesem Beispiel eines Diskontinuierungsverfahrens zeigt in dieser Formel den Wert von einem Euro an – der Betrag der investiert wird, um einen zukünftigen Wert zu erhalten. Dabei wird der aktuelle Wert niedriger, wenn der verwendete Zinssatz ansteigt. Werden in der Zukunft höhere Zinsen erwartet, dann muss man also gegenwärtig weniger investieren. Ist der Zinssatz bei der Diskontinuierung niedrig, dann muss mehr investiert werden, um in der Zukunft einen höheren Wert zu erhalten. Darüber hinaus gilt, dass der aktuelle Wert eines Betrags umso tiefer ist, je länger sich ein sogenannter Investitionshorizont erstreckt.

Bei dieser Art der Diskontinuierung wird nur ein konstanter Zinssatz verwendet und es wird davon ausgegangen, dass der Nominalwert zum Ende der Investitionszeit ausgezahlt wird und Couponzahlungen regelmäßig erfolgen. In der Praxis existiert auf dem Finanzmarkt jedoch eine solche Kontinuität häufig nicht und es kommt zu Schwankungen oder beispielsweise unregelmäßigen Zahlungsströmen. Dadurch wird eine Berechnung erschwert. Wenn die Investition beispielsweise mit einer Prämie zurückgezahlt wird, dann fällt nur der letzte Cash Flow nicht vollständig an, sondern entsprechend des Rückzahlungspreises. Erfolgt die Zinszahlung nicht im Rhythmus von einem halbe Jahr, dann wird die folgende Formel zur Berechnung herangezogen, wobei v die Tage zwischen dem Settlement und der nächsten Couponzahlung bezeichnet, CP den Call-Preis und n die Anzahl der Perioden:

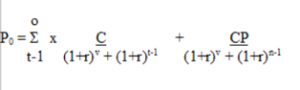
Bei Obligationen mit einer Rückruf-Option ist es möglich, dass der Emittent die Emission zu einem zuvor nicht berechneten Zeitpunkt zurückruft: Aufgrund der dynamischen Entwicklungen auf den Finanzmärkten ist zuweilen spontanes Handeln notwendig. Bei einer Rückruf-Aktion werden dabei auch die damit verbundenen Kosten berücksichtigt und genau abgewogen, ob sich eine Rückruf-Aktion bezüglich der Marktzinsen lohnt.

Die Analyse mehrerer Zinssätze

Die Zahlungsströme von rückrufbaren Obligationen können nicht mit Sicherheit bestimmt werden. Obligationen mit Optionen werden mit Multifaktor-Modellen bewertet. Deshalb werden dabei häufig mehrere Zinssätze im Laufe der Zeit untersucht. Nach dem Modell von Longstaff und Schwartz werden mehrere Zinsfaktoren für die Bewertung verwendet. Nach diesem Modell, das auf der Monte-Carlo-Simulation basiert, wird der sogenannte Continuation Value, der bei der Ausübungsentscheidung einer Option auftritt, mit Hilfe einer Regression festgelegt. In diese Regression fließen die Informationen aus allen simulierten Daten-Pfaden ein. Mit Hilfe dieses Verfahrens wird dann die optimale Stoppzeit geschätzt, auf die für den jeweiligen Pfad eine entsprechende Auszahlung folgt. Die Investitionszeit hat Auswirkungen auf aktuelle und zukünftige Werte. Die Verzinsung der entsprechenden Beträge wird grafisch dargestellt. Bei der Bewertung von Obligationen wird der Einfluss der jeweiligen Zinszahlungen berücksichtigt. Bei der Bewertung können jedoch jederzeit Schwierigkeiten entstehen.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Verschiedene Bewertungsmodelle

Darüber hinaus existieren zahlreiche Bewertungsmodelle amerikanischer Optionen. Bei der Bewertung werden Baum- und Finite-Differenzen-Methoden benutzt und die Anwendbarkeit von Simulationstechniken zur Preisbestimmung wird analysiert. Dazu wird zunächst eine Ausübungsstrategie festgelegt. Bei einer Simulation wird eine große Anzahl Pfade des Basiswertes dargestellt. Einem Pfad wird dann analog zur Ausübungsstrategie jeweils eine Auszahlung zugeordnet. Dadurch kann der faire Preis des Derivats bestimmt werden. Die Entwicklung des Basiswertes läuft bei der Bewertung in der Zeit vorwärts. Eine Ausübungsstrategie dient dazu, einen Preis zu berechnen. Bei Derivaten mit amerikanischer Ausübung liegen Berechnungsalgorithmen einer Rückwärtsinduktion zugrunde. Nach Richard Bellmann läuft die dynamische Programmierung in der Zeit rückwärts. Zudem wird die optimale Ausübungsstrategie in Bezug auf eine Stoppzeit zunächst durch Simulation ermittelt. Das Wissen über die logischen, mathematischen und rechtlichen Zusammenhänge ist vor der Marktteilnahme von großem Nutzen für die Marktteilnehmer, denn nur auf diese Weise können zu jeder Zeit die richtigen Entscheidungen und sinnvolle, nachhaltig nützliche Investitionen getätigt werden. Die verschiedenen Bewertungsmodelle können dabei individuell verwendet werden und beispielsweise zur Berechnung der verschiedenen Zinssätze dienen.

Aussagen über den aktuellen Wert des Geldes

Der Wert, den ein Marktteilnehmer heute investiert hat, ist nach einer Verzinsung grundsätzlich niedriger. Es muss bei Bewertungen immer beachtet werden, wie viele Zinsen man erhält oder abgezogen werden. Investitionen werden deshalb zudem auf eine Weise getätigt, die Zinssätze nachhaltig untereinander ausgleicht, sodass im besten Fall bereits durch die Zinsen Gewinn erzielt wird oder zumindest Verlust und Risiken vermieden werden. Geld, das man zurzeit besitzt ist mehr wert als Geld, das man in der Zukunft zurückerhält, denn das aktuelle Geld und der aktuelle Wert des Geldes sind sicher. Mit vollkommener Sicherheit kann letztlich zudem gar keine Aussage über einen Wert in der Zukunft getroffen werden. Es ist am wichtigsten, in jedem Moment durch genaue Analysen festzustellen, was zum gegenwärtigen Zeitpunkt benötigt wird und was im jeweiligen Moment die beste Investition darstellt. Die Bewertungen dienen dabei besonders der täglichen, aktuellen Bewertung der Liquidität eines Geschäftsteilnehmers. Ein Cashflow liefert Aufschlüsse darüber, ob und in welchem Maß ein Unternehmen Investitionen tätigen kann und dadurch auch in Zukunft in der Lage dazu sein wird, am Finanzmarkt teilzunehmen, in welcher Höhe Barmittel für die Tilgung von Schulden, Zinszahlungen und zur Ausschüttung an die Gesellschafter existieren und wie hoch die Insolvenzgefahr eingeschätzt werden kann. Der Konjunkturverlauf hat einen großen Einfluss auf Investitionen. Konjunkturelle Phasen des Abschwungs sind von verminderten Investitionen begleitet, Phasen des Aufschwungs und der Hochkonjunktur sind häufig von einer hohen Investitionstätigkeit geprägt. Investitionen sind bekanntermaßen die Voraussetzung für ein gleichmäßiges Wirtschaftswachstum und die Schaffung von Arbeitsplätzen. Je höher der Wert des Geldes ist, desto größer sind auch die Möglichkeiten, weitere Investitionen zu tätigen und am Finanzmarkt teilzunehmen. Geld scheint unvergänglich zu sein und wird deshalb zum Maß aller Dinge erhoben. Geld wird jedoch innerhalb des dynamischen Finanzmarktes weitertransferiert: Deshalb ist es wichtig, darauf zu achten, sich des zukünftigen Werts des Geldes nicht zu sicher zu sein.

Geld wird häufig als eine „gesellschaftliche Verabredung“ bezeichnet, die auf Prognosen basiert. Dem bedruckten Papier wird jedoch ein bestimmter Wert beigemessen, vor allem mathematisch. In Finanzkrisen stellt sich der aktuelle Wert des Geldes als gering dar. Es gilt dabei nicht, das Vermögen bis zur Sinnlosigkeit anzuhäufen, sondern auf eine sinnvolle Art weiterhin zu investieren, denn Geld einfach unendlich anzustauen, bedeutet in der Tat keine rationale Teilnahme am Finanzmarkt, auch wenn auf der anderen Seite nicht zu vorschnell gehandelt werden soll. Diese Faktoren kommen als Erschwernisse bei der Bewertung hinzu.

Geld gilt als eine Leidenschaft und hat sich über Jahrtausende innerhalb von allen Kulturen und Religionssystemen entwickelt. In der Gegenwart vollzieht sich ein blitzschneller Finanzhandel: In Sekundenschnelle werden weltweit Milliardenwerte angefordert und wieder abgegeben.

Die Diskrepanz zwischen der Gegenwart und der Zukunft

Die Entscheidungstheorie ist eine der bedeutendsten Theorien der gesamten Wirtschaftswissenschaften. Diese Theorie basiert auf der Annahme, dass eine Diskrepanz zwischen dem Wert, der in der Zukunft erwartet wird, und den aktuellen Gegebenheiten besteht. Die Theorie spielt beispielsweise bei Entscheidungen darüber eine Rolle, welcher Zinssatz von einem Kunden verlangt wird oder beispielsweise ob die zukünftigen Renditen ein zu großes Risiko bilden.

Erwartungswerte

Der Begriff des „Erwartungswertes“ wurde von Blaise Pascal in Paris und Pierre de Fermat in Toulouse geprägt. Die beiden hatten festgestellt, dass sich der Erwartungswert eines unsicheren Ereignisses berechnen ließ, indem man die möglichen Werte mit den Wahrscheinlichkeiten ihres Auftretens multiplizierte.

Nach Pascal und Fermat lässt sich der Gewinn am bekannten Beispiel des Münzwerfens wie im Folgenden berechnen: Die Wahrscheinlichkeit dafür, dass die Münze bereits beim ersten Wurf ihre Kopfseite zeigt, beträgt 1/2. Will man die Kopfseite erst beim zweiten Wurf sehen, so sinkt die Wahrscheinlichkeit dafür auf 1/4. Soll die Münze erst nach zwei Würfen mit dem Ergebnis Zahl auftauchen, dann wird die Wahrscheinlichkeit noch geringer. Der zu erwartende Gewinn ergibt sich aus der Summe der verschiedenen Ausschüttungen, die mit den Wahrscheinlichkeiten multipliziert werden.

Falsche Erwartungen und kein Gewinn

Das Ergebnis ist überraschend. Jedes der Produkte ergibt genau 1/2. Geht man nun von der Chance aus, dass der Spieler unzählige Male nacheinander eine Zahl wirft und das Ergebnis Kopf ausbleibt, muss der Wert 1/2 unendlich oft addiert werden. Der zu erwartende Gewinn wächst in diesem Fall ins Unendliche. Nach dem Mathematiker Gabriel Cramer ist der Nutzen einer zusätzlichen Goldmünze niemals null, falle aber immer geringer aus als für die vorherige – mit dem Vermögen steige also auch der Nutzen, doch dessen Zuwachsrate nehme immer weiter ab. Der Nutzen steigt mit der Quadratwurzel des Vermögens an, spekulierte Cramer und schätze den zu erwartenden Gewinn nun auf etwas mehr als 2,9 Dukaten. Andere Wissenschaftler argumentierten im Laufe der Geschichte der Wirtschaft, dass das Paradoxon nicht sei, dass der Nutzen für den Spieler ab einer bestimmten Gewinnsumme zu klein ausfalle, sondern dass der Spieler sehr geringe Gewinnchancen einfach außer Acht ließe. Demgemäß setzte Bernoulli alle Wahrscheinlichkeiten kleiner als 1/32 gleich null und erhielt einen zu erwartenden Gewinn von 2,5 Dukaten. Obwohl Cramers Argumentation genauso legitim war, zeigte er sich in seiner Antwort reuevoll. Es ist also unwahrscheinlich, aber möglich, dass zu jeder Zeit derselbe Gewinn erzielt wird.

Nach dieser Theorie wird der aktuelle Wert des Geldes auf seinen aktuellen Nutzen bezogen. Der Nutzen eines möglichen Gewinns kann zudem mit seiner Wahrscheinlichkeit multipliziert werden. Die Lösung des „Sankt-Petersburg-Paradoxons“ gilt als einer der grundlegendsten wissenschaftlichen Beiträge in den Wirtschaftswissenschaften. Mehr Geld ist zwar immer besser als weniger, es lohnt sich jedoch, auf Geld zu verzichten und dadurch Risiken zu vermeiden. Während Einzelne mit Billionen jonglieren, sucht ein Durchschnittsmensch Sicherheit, indem er sein Einkommen zu Vermögen machen will. Ein Notgroschen kann bekanntlich ein Versprechen sein, das nicht eingelöst werden kann. Nach einem Zusammenbruch des Finanzsystems kann man erkennen, dass Geld nicht arbeitet. Deshalb sind genaue mathematische Berechnungen umso wichtiger, denn dadurch können Aussagen getroffen werden, die überhaupt eine Kalkulation von Ereignissen in der Zukunft zulassen, die sich häufig oder aufgrund verschiedener zugrunde liegender Daten ergeben.

Erfolgreiches Zeit-Management

Erfolgreicher Finanzhandel an der Börse erfordert nicht nur die Berücksichtigung von Laufzeiten und Zukunftswerten, sondern auch die realistische Organisation der Gegenwart mit den zur Verfügung stehenden Mitteln und Investitionsmöglichkeiten. Auf einer Zeit-Skala steht die Zukunft mit der Gegenwart in Verbindung. Die Zukunft ist also das Ergebnis der Gegenwart. Dennoch unterscheiden sich die Zahlungsströme, Zinssätze und der Wert des Geldes in der Gegenwart von Werten und Beträgen in der Zukunft. In der Realität des Finanzmarkts existiert häufig keine Kontinuität und es kommt beispielsweise zu unregelmäßigen Zahlungsströmen. Durch diese Unregelmäßigkeiten wird eine Berechnung erschwert. Ein erfolgreiches Zeit-Management kann dabei helfen, die aktuellen und zukünftigen Werte und beispielsweise die dazugehörigen Termine genau zu strukturieren. Für ein erfolgreiches Zeit-Management gibt es zudem zahlreiche Planungstechniken, um rechtzeitige und vollständige Bewertungen durchführen zu können. Darüber hinaus dienen Strategien dazu, beispielsweise täglich Prioritäten bei den Berechnungen zu setzen oder Kosten zu berechnen. Die aktuellen und die zukünftigen Daten werden täglich erneut analysiert, weil sich die Werte in jedem Moment ändern können.