Preisnotierung – Die bedeutendsten Preismodelle und Indizes im Detail!

Die Preisnotierung ist essenziell, wenn es darum geht in eine fremde Währung zu investieren. Durch die Bestimmung der Preisnotierung kann der Investor ohne großen Aufwand herausfinden, ob eine Anlage lohnenswert sein kann oder nicht. Fraglich ist, wie genau die ausgewählten Preisnotierungen der selektierten Anlagen in eine Kennzahl implementiert werden können. Hierbei hilft die Lehre der Indizes: Im Rahmen dieser Analyse wird der Indizes des Preises sowie jener der Mengen betrachtet. Damit ist es möglich die Differenzen einer Region oder eines Landes miteinander vergleichen zu können. Durch die Angabe einer Preisnotierung können folgende Größen bestimmt werden:

– die Veränderung des Wohlstands

– die Bestimmung der Stabilität des Geldes

– die Bereinigung von Geldeinheiten

Die Preisnotierung ist bei der Bestimmung des Sozialprodukts sowie des privaten Verbrauchs elementar. Um erfolgreich auf dem Markt investieren zu können, darf die Notierung des Preises von Anlagegütern wie den Devisen keinesfalls fehlen.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die bedeutendsten Preismodelle und -indizes

Der Index nach „Étienne Laspeyres“ ermöglicht es dem Investor zu erschließen, ob eine Investition zum betrachteten Zeitpunkt teurer, günstiger oder gleich zum Referenzjahr ist. Nachteilig bei diesem Modell ist die Tatsache, dass neue Anlagegüter nicht berücksichtigt werden. Auch eine Änderung der gewählten Investitionsgüter führt zu der Problematik der unzureichenden Interpretierbarkeit. Die Errechnung dieses Gedankengangs ist jedoch einfach und ohne hohe Kosten ausführbar. Von Relevanz sind bei der Kalkulation die gegenwärtigen Preise. Somit wird sichergestellt, dass eine direkte Vergleichbarkeit der Indizes gewährleistet werden kann. Damit die Berechnung erfolgen kann, muss die nachfolgende Formel ausgeführt werden:

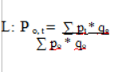
Das Ergebnis dieser Berechnung zeigt dem Investor den prozentualen Preisanstieg oder Preisverfall eines Gutes.

Damit herausgefunden werden kann, ob ein Investor mehr, weniger oder genauso viel für eine Anlage zahlen muss, im Vergleich zum Referenzzeitpunkt, ist die folgende Formel zu nutzen:

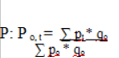
Im Vergleich zur vorigen Methode ist die Berechnung dieses Schemas eher zeitlich aufwendig, da jede Periode einzeln betrachtet werden muss.

Die Schlussfolgerung aus beiden Modellen. Bei der Betrachtung der Ergebnisse von beiden Schemen zeigt sich, dass jenes nach Laspeyres über höhere Indizes verfügt, wenn die Steigerung des Preises eintritt. Dies bedeutet, dass bei einer quantitativ steigenden Nachfrage mit einer relativen Senkung des Preises verbunden sein muss. Innerhalb des Modells von Laspeyres können diese Änderungen der Struktur aufgrund der konstanten Betrachtung jedoch nicht betrachtet werden.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Erfolgreiche Investitionen in Krisenzeiten der Wirtschaft

Damit ein Investor auch in Wirtschaftskrisen dazu in der Lage ist, rentable Anlagen zu erzielen, sollte dieser die unterschiedlichen Möglichkeiten betrachten. Vor mehr als 30 Jahren wurde angenommen, dass ein sich ausbreitendes geldpolitisches System nicht mit fixen Wechselkursen verknüpft werden kann. Aufgrund des Fehlens des Budgets des Staats in Verbindung mit einer Expansion der Menge des Geldes wird es zu einer Verringerung des Abgangs von Devisen kommen. Hierdurch muss auf dem Devisenmarkt mit finanziellen Mitteln eingegriffen werden, um die definierte Gleichheit bewahren zu können. Sind auf dem betreffenden Finanzmarkt keine Reserven und Devisen mehr vorhanden, kommt es zu einer Abwertung. Die Investoren haben folglich die Möglichkeit durch eine Spekulation auf dieses Geschehnis Gewinne zu erzielen. Basis der Annahme ist, dass das Angebot von Geld durch die Zentralbank adjustiert wird. Die Deckung des Angebots an Geld erfolgt mit Darlehen sowie Reserven aus dem internationalen Raum. Hierdurch ergibt sich folgende Annahme:

m = d + r

Die Kennzahl d basiert auf der Annahme, dass diese um eine fixe Rate μ steigt. Da die Nachfrage nach Geld in negativer Weise vom nominalen Zins abhängig ist ergibt sich:
m – p = α (i)

Hierbei bezeichnet der Buchstabe p den Exponenten des Preisniveaus sowie m jenen der Menge des Geldes. Somit gilt die totale purchasing power parity:

p = p* + e

p* = Exponent des internationalen Niveaus des Preises

e = Exponent des Kurses der Preisnotierung

Die Investoren können den nominalen Zins deshalb wie folgt errechnen:

i = i* + eo

i = nationales Niveau der Zinsen

i* = internationales Niveau der Zinsen

eo = Rate des Wachstums eines Kurses

Kann der Investor somit eine transparente Aussicht auf die Rate des Wachstums erhalten, sollte diese der Änderung des Kurses gleichzusetzen sein. Bei einer gesteigerten Menge an Geld kommt es generell zu einem Effekt der Zinssenkung. Außerdem üben die Geschäfte der Arbitrage eine Spannung auf den Kurs des internationalen Währungsmarktes aus. Damit die Gleichheit weiterhin fixiert werden kann, muss auf dem Devisenmarkt eingegriffen werden. Dies hat zur Folge, dass der Devisenkurs gestärkt wird. Im Rahmen einer Spekulation ist es ersichtlich, dass das konstante System des Kurses nicht beibehalten werden kann. Der Investor kann dies aus der nachfolgenden Formel erkennen:

d + r – p* – e = α (i*)

Damit der Anleger erfolgreich spekulieren kann, ist der wahre Wechselkurs zu bestimmen, damit ein Gewinn erreicht werden kann. Hierbei ist es wichtig aktiv zu werden, sobald der wahre Wechselkurs höher ist als der fix vereinbarte Wechselkurs. Da es im Rahmen dieses Vorgangs zu multiplen Investitionen kommt, ist der wahre Wechselkurs jener, welcher der konstanten Gleichheit entspricht. Der Wechselkurs wird somit durch die spekulativen Vorgänge in einem Rahmen gehalten. Als Grundsatz gilt, dass der Wechselkurs um den gleichen Faktor steigt wie der Mangel des Budgets. Unter der Annahme einer Gleichheit der Zinsen gilt, dass der nominale Zinssatz bei der Spekulation steigt. Auf dem Geldmarkt wird somit eine Ausgewogenheit durch das minimierte Angebot an Geld erzielt, welches den verloren gegangenen Reserven und der verringerten Nachfrage nach Geld entspricht. Dies liegt im ansteigenden nominalen Zinssatz begründet.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die Relation von Nutzen und Kosten

Im Rahmen dieses Modells erhält der Investor einen Einblick in das streng rationale Handeln unter der Beachtung des Verhältnisses von Nutzen und Kosten. Dies dient dazu abzuwägen, ob der fixe Kurs beibehalten oder aufgegeben wird. Auf der Basis dieser Theorie nutzt der Investor die zukünftigen Annahmen sowie die vorhandenen Daten. Es muss demnach nicht die mittelbare Schlussfolgerung sein sich von einem fixierten Kurssystem zu distanzieren, wenn die Politik des Geldes nicht stabil ist. Der Anleger sollte demnach aufgrund der gewünschten Effekte eine Schlussfolgerung bezüglich der eventuellen Abwertung treffen.

Für den Investor ist es wichtig zu wissen, dass die Geldbasis auf dem Markt nicht verändert werden muss, wenn festverzinste Wertpapiere gekauft oder verkauft werden. In diesem Fall wird das Eliminieren der konstanten Gleichheit eine direkte Auswirkung auf die Kennzahl d haben, welche abgewertet wird. Als Schlussfolgerung hieraus kann der Investor ziehen, dass der gleiche Effekt auf die Rate der Inflation gilt. Der Anleger sollte deshalb bei der Investition darauf achten, dass die unmittelbaren und mittelbaren Auswirkungen einer Entscheidung immer berücksichtigt werden.

Der Investierende kann somit erkennen, dass ein fixiertes System des Kurses dann nicht erfolgreich ist, wenn die Basisdaten von schlechter Qualität sind oder die Annahmen Charakter einer Selbsterfüllung aufweisen. Durch die qualitativ schlechten Basisdaten wird eine Abwertung eingelenkt, wodurch eine Inflation entsteht. Bei einer unsicheren wirtschaftlichen Lage ist eine Abwertung fraglich. Mithilfe des Charakters der Selbsterfüllung kann der Investor somit bei einer angenommenen Herabsetzung erwarten, damit der nominale Lohn steigt. Weitere negative wirtschaftliche Auswirkungen führen dazu, dass ein Verlassen des fixen Systems der Kurse als Lösung angesehen wird. Dies bedeutet, dass das Erwarten einer Herabsetzung dazu führt, dass diese auch stattfindet.

Die einfache Berechnung der Wachstumsrate

Nachdem die Basis der Wachstumsrate identifiziert ist, kann diese zur Berechnung der Rate des Wachstums genutzt werden. Zur Definition der Basis der Wachstumsrate werden Daten benötigt, welche aufgrund des zeitlichen Aspekts eine Unterscheidung in der Quantität erfahren. Der Investor benötigt zur Errechnung der Rate des Wachstums lediglich zwei Werte. Beträgt der Wert einer Anlage in einer Periode x 100 Euro und zum heutigen Zeitpunkt 110 Euro, ist die Basis der Wachstumsrate 100. Der Endwert beziehungsweise heutige Wert beträgt 110. Würden beide Werte 100 betragen bedeutet dies eine Rate des Wachstums von null. Wird über einen längeren Zeitraum der Faktor des Wachstums betrachtet und dieser zeigt sich linear, dann ist von einer konstanten Wachstumsrate zu sprechen.

Damit die Wachstumsrate ermittelt werden kann, ist folgende Formel im Rahmen des Beispiels zu nutzen:

(110 – 100) = Rate des Wachstums in Prozent

100

In dem angegebenen Beispiel würde die Wachstumsrate somit zehn Prozent betragen. Als Pendant zu dieser positiven Rate des Wachstums gibt es noch jene, welche als negativ zu bezeichnen ist. Dies bedeutet, dass der vergangene Wert in diesem Fall den aktuellen Wert übersteigt und somit zu einem negativen Ergebnis führt.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Das Berechnen der Wachstumsrate über mehrere Perioden [Preisnotierung]

Essenziell zur Errechnung der Rate des Wachstums über mehrere Perioden ist eine Formel, welche alle der gewünschten Intervalle berücksichtigt. Der Investor hat den Vorteil, dass die Einheit der Perioden keinen Einfluss auf die Zuverlässigkeit der nachfolgenden Formel hat. Deshalb ist es möglich Perioden oder Intervalle von Monaten, Tagen, Jahren oder Sekunden zu wählen.

Zur Kalkulation der angestrebten Wachstumsrate benutzt der Anleger die folgende Formel:

Gegenwärtiger Wert = (Wert der Vergangenheit) * (1 + Rate des Wachstums)n

Diese Gleichung lässt sich wie folgt umformen:

Rate des Wachstums = (gegenwärtiger Wert / Wert der Vergangenheit) 1/n – 1.

Im Anschluss an die Berechnung erhält der Investor die durchschnittliche Wachstumsrate für die betreffenden Intervalle der Zeit. Dies geschieht jedoch auf der Basis der Annahme der konstanten Rate des Wachstums.

Die Anwendung der jährlichen Wachstumsrate [Preisnotierung]

Bei der Anlage in Anleihen müssen Investoren eine Vielzahl von Faktoren berücksichtigen, damit die Investition erfolgreich ausgeführt werden kann. Bei der Betrachtung von beispielsweise Investmentfonds können Anleger die durchschnittliche Rendite mithilfe der jährlichen Wachstumsrate betrachten. Zudem kann die Rate des Wachstums über ein bestimmtes Intervall dazu gebraucht werden Leistungen zu vergleichen und diese zu präsentieren, was im Geschäft mit Finanzen notwendig ist. Durch die Aufbereitung vergangener Daten können die Ergebnisse dazu genutzt werden Anleihen mit Aktien oder die Aktien mit dem persönlichen Sparbuch zu vergleichen. Voraussetzung zur Anwendung der jährlichen Wachstumsrate ist, dass eine Anlage mit der gleichen Geschwindigkeit zunimmt. Da diese Theorie jedoch stark von der Realität abweicht, ist die jährliche Rate des Wachstums ein nicht reales Modell.

Die Nach- und Vorteil der jährlichen Wachstumsrate für Anleger [Preisnotierung]

Die Benutzung der Rate des Wachstums ist vorteilhaft, wenn unterschiedliche Anlagen über einen bestimmten Zeitraum betrachtet und ausgewertet werden sollen. Hierdurch lässt sich ein optimales Portfolio errichten, welches dazu führt, dass der Investor eine gewünschte Rendite unter geringem Risiko erzielen kann. Zudem ist die jährliche Rate des Wachstums eine Möglichkeit das Verhältnis von Risiko und Ertrag eines Wertpapiers im Vergleich zu einem anderen Wertpapier zu bestimmen.

Nachteilig bei der Betrachtung des Konzepts ist die Annahme einer konstanten Wachstumsrate. Auf realen Märkten herrscht natürlicherweise eine Schwankung, welche dazu führt, dass die Ergebnisse einer Investition über eine bestimmte Periode abweichen. Die Berücksichtigung dieser Schwankungen ist im Rahmen der Abschätzung eines Risikos für den Anleger essenziell und sollte nicht außer Acht gelassen werden. Zudem sollte der Investierende berücksichtigen, dass die Basis der Errechnung der jährlichen Wachstumsrate historische Werte sind. Dies bedeutet, dass vergangene Werte nicht immer auf eine zukünftige Entwicklung schließen lassen, da die Entwicklung einer Anlage in der Zukunft von unterschiedlichen variablen Faktoren abhängig ist. Außerdem ist es möglich als Anfangswerte jenen Wert einzusetzen, welcher als gering eingestuft werden kann, um de Rate des Wachstums zu erhöhen und den Investor hiermit zu beeindrucken.

Jetzt zum Testsieger Trive!64% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit Trive Financial Services Malta Ltd.

Die Wachstumsrate und deren Verhalten – Wissenswertes für Anleger [Preisnotierung]

Bei der Stärkung des Finanzmarktes gibt es mehrere Möglichkeiten, wie sich diese auswirken können. Hierzu zählt, dass sich bei gleichbleibenden Einnahmen die Ausgaben reduzieren lassen. Außerdem besteht die Option, dass die Ausgaben konstant bleiben die Einnahmen jedoch steigen. Auf der Basis dieser Theorien gibt es für den Anleger vier zu beachtende Auswirkungen. Tritt eine dieser Wahrscheinlichkeiten ein, kann die Rate des Wachstums konstant sein. Hierbei ist es erforderlich, dass die Nachfrage einen Rückgang erlebt. Durch die hieraus resultierenden niedrigeren Ausgaben des Staats kommt es zu einer höheren Nachfrage auf ausländischen Märkten. Eine weitere Option ist, dass die Wachstumsrate auf lange Sicht sinkt, wenn die Einnahmen steigen, die Quote des Staats jedoch gleich bleibt. Zudem ist es möglich, dass die Wachstumsrate langfristig ansteigt, wenn der Kapitalmarkt eine positive Zukunft erschließen lässt, weshalb die Ausgaben des Staats reduziert werden können. Ebenso eine Möglichkeit ist das Auslösen eines Antriebs zur Ankurbelung des Wachstums am Kapitalmarkt.