Kupon, Rendite und Preis im Bezug auf die halbjährlichen Zinszahlungen

Die Basis des erfolgreichen Investierens

Damit der Anleger erfolgreich investieren kann, ist es nötig den Zusammenhang und die Unterschiede zwischen Kennzahlen wie der Rendite und dem Preis einer Anlage zu erkennen. Wird zu dem Zeitpunkt t eine Anlage mit dem Preis Pt erworben, erwartet der Anleger zukünftige Auszahlungen im positiven Bereich. Diese Auszahlungen können fix oder variabel sein und an einem einzigen oder an multiplen Zeitpunkten durchgeführt werden.

Bei der Rendite einer Investition kann diese entweder stetig oder diskret diskontiert werden. Die Betrachtung der diskreten Rendite zeigt, dass diese zu einem Zeitpunk t von dem Preis einer Anlage Pt sowie den erwarteten Auszahlungen Ct+i abhängig ist. Deshalb gilt die folgende Formel zur Bestimmung des Preises zum Zeitpunkt t:

            Ct+i
Pt = ∑ ——
       i ∈ I (1 + R)i

Beträgt jeder der Auszahlungen null, dann gilt, dass die Rendite = – 1 ist, da diese so definiert ist, dass der diskontierte Wert von der Auszahlung auf den gegenwärtigen Preis gerechnet werden muss. Dies bedeutet, dass die Diskontierung sich auf die Verzinsung in diskreter Form bezieht. Im Rahmen dieser wird der Ertrag aus den Zinsen zum Ablauf einer definierten Periode vergütet. Wird dieser Ertrag aus Zinsen kontinuierlich angelegt, ist es möglich mit einem niedrigeren stetigen Zins die stetige Rendite namens r zu erzielen. Der Investor kann die stetige Rendite mit der folgenden Formel errechnen:

er = 1 + R

Infolgedessen kann auch die zuvor bestimmte Gleichung adjustiert werden:

Pt = ∑     Ct+i e-ir
i ∈ I

Beträgt die Rendite null, dann hat die diskrete und die stetige Rendite den gleichen Wert. Für jeden anderen Fall ist die diskrete Rendite höher als die stetige Rendite.

Jetzt zum Testsieger XTB!CFDs sind komplexe Instrumente und gehen wegen der Hebelwirkung mit dem hohen Risiko einher, schnell Geld zu verlieren. 77% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit diesem Anbieter. Sie sollten überlegen, ob Sie verstehen, wie CFDs funktionieren, und ob Sie es sich leisten können, das hohe Risiko einzugehen, Ihr Geld zu verlieren.

Die Bestimmung der einmaligen Rendite

Wird eine Rendite ein einziges Mal nach dem Ablauf der Periode n ausgezahlt, kann die diskrete Rendite von dem Investor mithilfe folgender Formel bestimmt werden:

             Ct+n
Pt =  ———-
             (1 + R)n

Für die stetige Rendite kann eine Abwandlung abfinden:

Pt = Ct+n e-nr

In der Regel wird die Rendite auf der Basis der Referenzperiode gewählt, wobei es unwichtig ist, wann die Auszahlung erfolgt.

Werden beispielsweise fix verzinste Wertpapiere wie die Nullkuponanleihe betrachtet, zeigt sich nach dem Abschluss der Laufzeit mit n Intervallen die Auszahlung in Höhe von Ct+n = 1. Die Rendite der Nullkuponanleihen ist als Zinsstruktur bekannt, die sich in Relation zu der Laufzeit gestaltet.

Das Bestimmen der Rendite in Perioden

Möchte der Anleger die Rendite mit einer einmaligen Auszahlung von beispielsweise einer Aktie betrachten, kann dies mithilfe der innerhalb der fortlaufenden Perioden erzielten Veränderungen des Preises umgesetzt werden. Hierbei wird der Preis der Aktie mit Pt, die Rendite mit Rt und die diskrete Rendite mit t bezeichnet. Zur Errechnung der Rendite muss der Anleger somit folgende Gleichung lösen:

            Pt

Rt = ———— -1
            Pt-1

Die Rendite in stetiger Form kann somit von dem Investor wie folgt errechnet werden:

rt = In (1 + Rt) = In Pt – In Pt-1

Der Anleger sieht von dem Bezug auf eine Referenzperiode bei dieser Berechnung ab und analysiert die einzelnen Zeitreihen der Preise. Hierbei ist es zum Beispiel möglich, die Rendite in folgenden Intervallen zu betrachten:

– Tage

– Wochen

– Stunden

– Monate

Die diskrete Rendite einer Periode Rt (k) kann somit als Rendite aus der Preisveränderung Pt-k auf jene mit der Bezeichnung Pt* mit der Basis des Intervalls k bezogen werden. Für Rt (k) lässt sich somit folgende Formel verwenden:
                Pt – Pt-k
Rt (k) =  ———
                  Pt-k

Zudem hat der Investierende die Option statistische Rechenverfahren zu nutzen, um aufeinander basierende Prozesse besser abzubilden. Damit die Rendite von beispielsweise Wertpapieren einfacher bestimmt werden kann und besser zum Vergleich geeignet ist, kommt es zur Umrechnung der gewünschten Zeitabschnitte zu jährlichen Renditen. Hierdurch kann ein Vergleich mit der risikofreien Rendite von einem bestimmten Wertpapier zügiger durchgeführt werden. Damit der Anleger die Umrechnung der periodischen Rendite in eine jährliche Rendite durchführen kann, ist zu beachten, dass dies nur unter der Annahme möglich ist, dass die Rendite innerhalb von einem Jahr stetig ist. Im nachfolgenden Beispiel kann der Investor erkennen, wie eine Umrechnung erfolgt.

Hierzu wird die wöchentliche Rendite betrachtet, welche auf das Jahr gerechnet mit 52 Börsenwochen bezeichnet wird. Deshalb ist die Rendite pro Woche Rt (x) wie folgt zu verjährlichen:
Rt (x) = (1 + Rt (x)) 52 -1

Würde die gewählte Rendite in Tagen errechnet werden müssten hierfür 250 als Basis dienen.

Jetzt zum Testsieger XTB!CFDs sind komplexe Instrumente und gehen wegen der Hebelwirkung mit dem hohen Risiko einher, schnell Geld zu verlieren. 77% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit diesem Anbieter. Sie sollten überlegen, ob Sie verstehen, wie CFDs funktionieren, und ob Sie es sich leisten können, das hohe Risiko einzugehen, Ihr Geld zu verlieren.

Kupon: Die festverzinslichen Anleihen und deren Rendite

Damit der Anleger bei der Wahl einer fix verzinslichen Anleihe die Rendite beziehungsweise den Preis bestimmen kann, muss dieser zwischen Anlage mit einer einzelnen Auszahlung oder jenen mit fixierten Intervallen unterscheiden. Bei der Nullkuponanleihe erhält der Investor nach dem Laufzeitende eine sichere Auszahlung.

Bei der Anschauung der Nullkuponanleihe werden die sogenannten Doppelindizes genutzt. Dabei stellt der primäre Index die restlich Laufzeit dar und der sekundäre Index den Zeitpunkt der Bewertung. Der Preis zum Zeitpunkt t wird mit P nt und die Auszahlung mit t + n benannt. Die Yield to Maturity ergibt sich für den Anleger aus folgender Rechnung:

Rendite (stetig) In P nt = – ny nt
                                                      1
Rendite (diskret) P nt =    ———
                                                (1 + Y nt) n

Der Investor sollte darauf achten, dass das elastische Verhalten des Preises P nt im Rahmen der Adjustierung der Rendite (1 + Y nt) mit der negativ aspektierten Laufzeit deckungsgleich ist. Dies bedeutet, dass die Nullkuponanleihe bei einer Veränderung des Niveaus des Zinssatzes unter der Annahme einer steigenden Laufzeit deutlich elastischer wird. Zu dem gewählten Zeitpunkt kann deshalb der Preis unter Beachtung des auszahlbaren Geldbetrags t + n (Faktor des Diskonts) mit nachfolgender Formel bestimmt werden:

                      1
P nt =   ————–
              (1 + Y nt) n*

Die Spannbreite des Zinses ist somit einfach durch den Anleger mithilfe der folgenden Kalkulationen berechenbar:

Rendite (diskret) S nt = Y nt – Y 1t

Rendite (stetig) S nt = y nt – y 1t

Die Struktur des Zinses ( Y nt/ y nt) verläuft normal, wenn t (Strukturkurve des Zinses) stetig steigt. Dies bedeutet, dass der Zins mit ansteigender Laufzeit zunimmt. Kommt es zum stetigen Fall der Strukturkurve des Zinses, sind die kurzfristigen Zinsen höher als jene über längere Zeit. Flache Strukturkurven zeichnen sich hierdurch aus, dass der Zinssatz konstant ist. In der Praxis ist es jedoch auch möglich, dass die Strukturkurve sich aus mehreren Varianten zusammensetzt.

Aufgrund der Relation von P nt und Y nt oder y nt und P nt ist die Struktur des Zinses mit der diskontierten Funktion zu beschreiben, welche sich auf die Laufzeit n bezieht.

Die Forward Rate und die periodische Rendite

Ist der Anleger darauf bedacht die Forward Rate beziehungsweise die periodische Rendite einer Null Kupon Anleihe zu bestimmen, sind folgende Annahmen zu beachten. Die Rendite einer Periode wird mit Rn, t + 1 benannt. Die Änderung des Kurses der Anleihe ist mit P n-1, t + 1 definiert, weshalb für die konstante Rendite einer Periode gilt:

                             P n – 1, t + t            (1 + Y nt) n
1 + R n, t + 1 =  ————–   =  ————————
                                 P nt                      (1 + Y n – 1, t + 1) n – 1

Für die stetige Rendite der Periode gilt:

y nt – (n – 1) (y n – 1, t + 1 – y nt)

Der Anleger kann somit sehen, dass eine Rendite größer eins als unsicher gilt. Die überschüssige Rendite (r n, t + 1 – y 1t) ist somit von der Änderung des Zinses
( y n – 1, t + 1 – y nt) sowie der Spanne des Zinses S nt = y nt – y 1t) abhängig, weshalb:

R n, t + 1 – Y 1t = S nt – (n – 1)(Y n – 1, t + 1 – y nt)

Die Rendite y nt einer Nullkuponanleihe, welche eine Laufzeit von n Perioden hat, ist deshalb der Mittelwert der Rendite der Perioden.

Die Forward Rate wird mit F nt benannt und unter der Annahme der Unmöglichkeit der Arbitrage angewandt, wodurch sich eine Zahlung n mit der Relation P n + 1, t/ P nt auf der Basis der Faktoren der Diskontierung mit der Laufzeit n + 1 ergibt. Der Anleger kann somit den Zusammenhang zwischen der Nullkuponanleihe und der Forward Rate in der nachfolgenden Gleichung erkennen:
                    P n, t             (1 + Y n + 1, t) n + 1
1 + F nt =  ———  =    ————————-
                   P n + 1, t                 (1 + Y nt) n
Damit die Relation verdeutlicht werden kann, wird die Forward Rate durch den Erwerb und die Verschuldung in der Nullkuponanleihe präsentiert werden. Der Erwerb einer Nullkuponanleihe hat eine Laufzeit von n + 1 und einen Preis von P n + 1, t sowie die Zahlung t + n + 1. Hieraus folgt, dass die Zahlung mit dem Wert P n + 1, t/P nt zu dem Zeitpunkt t + n auszuführen ist.

Die Struktur des Zinses kann mithilfe der Forward Rate F nt gezeigt werden. Dies bedeutet, dass die dargestellte Gleichung die Funktion der diskontierten Funktion zeigt sowie F nt, weshalb es dem Investor ermöglicht wird folgende Schlussfolgerung zu ziehen:

                             P nt
P n + 1, t =   ——————
                         1 + F nt

Für die stetige Forward Rate gilt deshalb:

f nt = y n +1, t + n(y n + 1, t – y nt)

Die Kupons und das Verhältnis zu Rendite und Preis

Der Anleger kann bei der Betrachtung von Kupons den Zusammenhang dieser mit der restlichen Laufzeit, dem definierten Zeitpunkt sowie den Indizes erkennen. Zur Erleichterung des Erkennens der Zusammenhänge wird der nominale Wert mit einer Einheit gezeigt. Die Zahlung des Kupons erfolgt somit in t + i wobei K i = C. Im Rahmen der Fälligkeit t + n ergibt sich somit K n = 1 + C. Der zum betreffenden Zeitpunkt t eingezahlte Preis beträgt P Cnt.

Die Kuponanleihe ist deshalb als eine Ansammlung von Nullkuponanleihen mit verschiedenen Laufzeiten anzusehen, weshalb auf einem ohne Arbitrage funktionierenden Markt gilt:

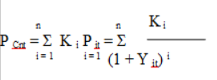
Basis dieser Annahme ist, dass die Zahlungen der betreffenden Intervalle mit dem passenden Zinssatz Y it der zugehörigen Laufzeit i diskontiert werden. Hierdurch kann der Investor die interne Rendite problemlos mit folgender Formel bestimmen: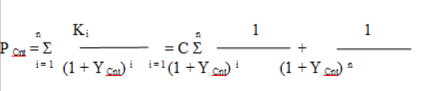

Tritt der Fall ein, dass n = 1, bedeutet dies, dass der Anleger Y C 1t = Y lt annehmen darf. Ansonsten ist die Rendite als Verhältnis von dem Preis des Kupons und dem Anteil mit

C

———-

P Cnt

zu ermitteln.

Jetzt zum Testsieger XTB!CFDs sind komplexe Instrumente und gehen wegen der Hebelwirkung mit dem hohen Risiko einher, schnell Geld zu verlieren. 77% der Kleinanlegerkonten verlieren Geld beim CFD-Handel mit diesem Anbieter. Sie sollten überlegen, ob Sie verstehen, wie CFDs funktionieren, und ob Sie es sich leisten können, das hohe Risiko einzugehen, Ihr Geld zu verlieren.

Kupon: Der Preis einer Kupon Anleihe

Nachfolgend erhält der Investor einen Überblick zwischen der Abhängigkeit der Laufzeit von dem Zinssatz einer Anleihe. Zu berücksichtigen ist, dass die Kennzahl Y Cnt hierzu nicht einfach genutzt werden kann, da diese von der Höhe der Kupons sowie der Laufzeit abhängt. Werden Kuponanleihen mit sich entsprechender restlicher Laufzeit angesehen, welche jedoch zu anderen Zeiten ausgegeben wurden, weshalb die Höhe der Kupons abweichend ist, kann der Nominalwert sowohl ober- als auch unterhalb von eins liegen. Zur Folge hätte der Anleger verschieden hohe interne Renditen. Es zeigt sich der Zusammenhang, dass bei einer klassischen Strukturkurve des Zinses eine niedriger interne Rendite für Anleihen mit großem Kupon ergibt, wohingegen eine hohe interne Rendite erzielt wird, wenn der Kupon niedrig ist. Dies liegt darin begründet, dass die kurzfristigen Zinsen bei höheren Kupon Zahlungen eine höhere Gewichtung im Rahmen der Definition der Rendite erhalten als jene mit niedrigeren Kupon Zahlungen. Der Anleger hat jedoch auch die Möglichkeit eine Kupon Anleihe zum Nominalwert zur Bestimmung der internen Rendite zu nutzen, umso ein eindeutiges Ergebnis zu erhalten. Diese Anschauung billigt es dem Betrachter davon zu profitieren, dass die interne Rendite dem Kupon der Anlage entspricht.

Mithilfe von diesem Wissen kann sich der Investor erklären, dass bei einer klassischen Kurve der Zinsstruktur die Strukturkurve des Kupons unterhalb jener des Zinses befindlich ist. Wird die inverse Strukturkurve des Zinses angeschaut, ist zu sehen, dass die Strukturkurve des Kupons oberhalb der Strukturkurve des Zinses rangiert. Zudem ist festzustellen, dass bei einer inversen Struktur des Zinses auch die zugehörige Struktur des Kupons invers ist. Gleiches gilt für die normale Strukturkurve des Zinses beziehungsweise Kupons.