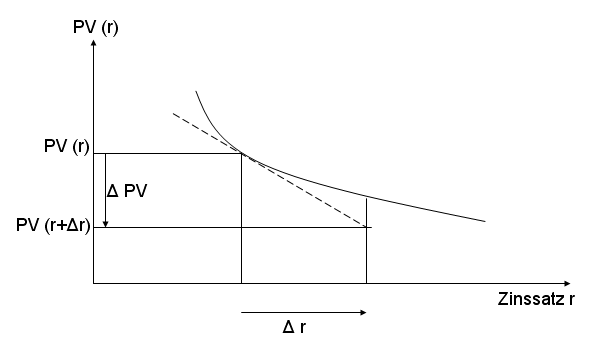
Konvexität Duration – Die Bestimmung von Preisveränderungen im Ratgeber!

Zuletzt aktualisiert & geprüft: 14.11.2019

Inhaltsverzeichnis Anzeigen

Die Preisveränderung von kurz- bis langfristigen Anlagegütern

Durch Anleihen und Obligationen kann beispielsweise ein betreffendes Unternehmen eine kurz- bis langfristige Finanzierung durchführen. Da die Anleihen auf dem Markt gehandelt werden, werden diese von unterschiedlichen Faktoren des Marktes in unterschiedlicher Intensität beeinflusst. Der Preis einer Anleihe wird jedoch durch die Nachfrage nach dieser und das Angebot der Anleihe bestimmt. Außerdem ist der Marktzins am Kapitalmarkt ein elementarer Faktor des Preises. Hierbei gilt, dass ein steigender Marktzins am Kapitalmarkt dazu führt, dass der Anleihenkurs fällt. Sinkt der Marktzins am Kapitalmarkt, steigt der Kurs einer Anleihe. Wird der Anleihenkurs zum Ausgabezeitpunkt betrachtet, erhält der Investor eine bestimmte Verzinsung pro Jahr auf diese Anleihe.

Bei einem steigenden Anleihenkurs würde dies bedeuten, dass alle gegenwärtig emittierbaren Anleihen einen entsprechend höheren Zinssatz für Investoren offerieren, was dazu führt, dass die Nachfrage dieser Anleihe steigt. Zur gleichen Zeit sinkt die Nachfrage nach der in der Vergangenheit erworbenen Anleihe, welche einen sinkenden Kurs verzeichnet hat. Für den Anleger bedeutet dies jedoch nicht, dass die Anleihe schnellstmöglich verkauft werden muss, denn die geringeren Zinsen führen häufig nur zu einer Minimierung der Rendite des Anlagegutes. Da das Niveau des Marktzinssatzes gestiegen ist, kommt es zu einer Änderung der angestrebten Verzinsung. Dies führt dazu, dass die ausgegebenen Zinsen ein steigendes Niveau im Rahmen der Anlage offerieren. Bei einer Steigerung des Marktzinssatzes am Kapitalmarkt wird der Wert einer Anleihe reduziert. Der Terminal Value wird jedoch durch das Wiederanlegen der entrichteten Zinsen zum Ausgleich gebracht.

Jetzt zum Testsieger eToro!74% der Konten von Kleinanlegern verlieren Geld beim Handel mit CFDs bei diesem Anbieter. Sie sollten sich überlegen, ob Sie das hohe Risiko, Ihr Geld zu verlieren, eingehen können. Krypto-Investitionen werden von eToro (Europe) Ltd. angeboten und die Verwahrung wird von eToro Germany GmbH durchgeführt. Ihr Kapital ist gefährdet.

Die Bestimmung von Preisveränderungen – die Duration und die Konvexität

Durch die Änderung eines Zinssatzes kann der Preis einer Anleihe definiert werden. Dies ist jedoch in einem aufwendigen Verfahren, der Errechnung des Barwertes, ausführbar. Die Änderung des Preises ist mithilfe der Konvexität und Duration limitiert abzuschätzen. Durch die Betrachtung der Duration kann die Elastizität des Zinskurses aufgezeigt werden. Dieser zeigt bei der Analyse, wie stark der Preis einer Anleihe bei einer gewissen Änderung des Zinses reagiert. Bei größeren Zinsänderungen unterschätzt die Duration den Preis einer Anlage jedoch, was an der Ungenauigkeit der Ergebnisse der Duration liegt. Diese sind darin begründet, dass die Duration annimmt, dass die Änderung von dem Kurs und den Zinsen linear erfolgt. In der Praxis tritt diese Annahme jedoch nicht ein, da Zins und Kurs sich konvex verhalten. Deshalb ist die Konvexität ein genaueres Mittel zur Optimierung der Abschätzungen. Die Konvexität steht für die Krümmung der Kurve des Preises und zeigt, wie sich eine Zinsänderung auf die Duration auswirkt. Bei einer starken Änderung des Zinssatzes kann es hilfreich sein, weitere Kennzahlen des Finanzbereichs zur Berechnung des Preises zu nutzen, um ein genaueres Ergebnis zu erzielen. Bei einer geringeren Änderung des Zinssatzes ist es jedoch nicht nötig diese Kennzahlen zu verwenden, da diese zu einem nahezu deckungsgleichen Ergebnis im Vergleich zur Berücksichtigung der Konvexität führen würden. Bei der Schätzung des Preises ist es zudem hinderlich, wenn sich die Zinssätze durch differierende Laufzeiten ungleichmäßig verhalten. Hierdurch wird die Steigung der Kurve des Zinssatzes geändert.

Das Errechnen von der Duration

Durch die Duration lässt sich das Risiko der Änderung des Zinses von Anleihen durch den Ausschluss von definierten Bedingungen durchführen. Die Berechnung der Duration fasst somit die folgenden Aspekte in einer einzigen Zahl zusammen:

– die Zinsen- und Tilgung (t)

– die Zahlungen (Zt)

– den Zeitpunkt

In einer Formel ausgedrückt bedeutet dies:

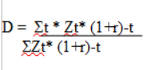
r = Rendite des Marktes

D = Duration

Hierbei ist zu beachten, dass die Tilgung beziehungsweise der Zins mit dem gegenwärtigen Wert der Zahlungen in Relation gesetzt wurde. Der hierdurch entstandene Wert wird durch die Gesamtheit aller Barwerte dividiert. Dies bedeutet für die Kennzahl (Duration), dass diese die Bindungsdauer im Durchschnitt angibt.

Die Formel zeigt, dass bei einer fix verzinsbaren Anlage eine Art Immunisierungseffekt auf das Änderungsrisiko des Zinssatzes erzielt wird. Dies bedeutet, dass der variable Zinssatz den Endwert im Rahmen einer Investition nicht beeinflusst. Bei einem sinkenden und fallenden Zins kann der Investor einen steigenden Kurs verzeichnen, welcher die erneute Verzinsung der Anlage nicht negativ aspektiert. Als Grundsatz gilt, dass die Duration den Wert der Laufzeit niemals übersteigen kann. Bei einer Abzinsung beträgt die restliche Laufzeit die durchschnittliche Dauer der Bindung. Dies liegt daran, dass innerhalb der Laufzeit nicht gezahlt wird, lediglich am Laufzeitende. Durch Einzahlungen kann die Höhe der Duration beeinflusst werden. Werden multiple Einzahlungen ausgeführt, erniedrigt sich die Duration dementsprechend. Auch der Zeitpunkt der Einzahlung beeinflusst die Duration somit. Eine lange Laufzeit geht somit mit einer steigenden Duration einher. Hierbei ist jedoch zu beachten, dass die Abschläge sich folglich reduzieren. In einem Portfolio implementierte fix verzinste Anlagen führen zu einer Duration, welche die Gesamtheit aller Anlagen abbildet. Diese werden mit dem passenden Anteil in Bezug auf den Wert am Markt gewichtet. Hierbei ergibt sich folgende Formel:

Die Effektive Duration und deren Berechnung

Die Effektive Duration wird dann angewendet, wenn die Strukturkurve des Zinses nicht flach ist. In der Formel für die Duration werden die jeweiligen Zahlungen von Zinsen mit den passenden Spotzinssätzen abgezinst. Hierdurch kommt es zu einer realitätsnäheren Konzipierung der Strukturkurve des Zinses. Jedoch kann auch bei dieser Art der Berechnung das Niveau des Zinssatzes lediglich um einen fixen Teil verschoben werden. Ebenso wie bei der klassischen Errechnung der Duration ist auch im Rahmen der Effektiven Duration die Genauigkeit abnehmend, wenn der Zinssatz eine starke Änderung erfährt. Eine detailliertere Betrachtung der Struktur des Zinses ist somit in Geschäften wie beispielsweise dem Bilanzstrukturmanagement und dem Sicherungsgeschäft nötig. Die Effektive Duration kann mit folgender Formel ermittelt werden:

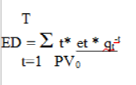
Die Key Rate Duration und deren Berechnung

Bei der Betrachtung der Key Rate Duration zeigt sich, dass hier nicht die komplette Strukturkurve der Zinsen bewegt wird, sondern lediglich die einzelnen Key Rates. Im Rahmen der Nutzung der Key Rate Duration kann diese auf die entsprechenden Anlagen ausgerichtet werden. Auch ein Rückgriff auf Erfahrungswerte kann die Analyse mithilfe der Key Rate Duration erfolgreich gestalten. Generell muss erwähnt werden, dass die Optimierung von Key Rates die Zinsumgebung beeinflusst. Dieser beeinflussende Faktor kann proportional abnehmen und durch das Erlangen der Grenzen der Key Rates eliminiert werden. Von besonders großer Auswirkung auf die Zinsumgebung sind die zeitlichen Abgrenzungen innerhalb der Key Rates. Die Spielräume innerhalb der Key Rates können individuell in Orientierung an finanziellen Vorgängen festgelegt werden.

Die Formel zur Errechnung der Key Rate Duration lautet wie folgt:

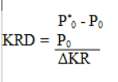
Das Errechnen von der Konvexität

Damit der Investor die genaue Veränderung des Preises abschätzen kann, wenn sich der Zinssatz einer Anlage am Markt verändert, wird die folgende Formel genutzt:

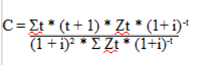
Die Abkürzung C steht im Rahmen dieser Formel für die Konvexität.

Ist die Konvexität hoch beziehungsweise positiv, reagiert der Kurs einer Anleihe wenig auf ansteigende Renditen. Jedoch reagiert der Kurs stark auf eine etwaige Senkung des Zinssatzes. Besitzt ein Investor zwei Anleihen mit einander entsprechenden Modifizierten Durationen wählt dieser jene mit der höheren Konvexität. Dies liegt daran, dass etwaige Verluste im Rahmen von Kursschwankungen reduziert und die Gewinne gesteigert werden.

Ist die Konvexität negativ, sind die Gewinne bei einem steigenden Zins eher niedrig und die Verluste sehr hoch.

Das Management des Portfolios und die Konvexität im Portfolio

Sowohl die Konvexität als auch die Duration sind im Rahmen eines erfolgreichen Managements des Portofolios essenziell. Durch die Duration des Portfolios ist es möglich einen Mittelwert aus allen Durationen errechnen zu können. Dies ist ebenso bei der Konvexität möglich. Im Rahmen des Portfoliomanagements besteht deshalb die Möglichkeit eine gewisse Anzahl an Anleihen zu besitzen, welche nicht auf Zinsschwankungen reagieren. Bei dem Management des Portfolios ist es wichtig eine gute Platzierung auf der Kurve des Zinses zu erhalten, was jedoch von den abgeschätzten Änderungen des Zinssatzes abhängt. Hierbei kommt es zu einer starken Gewichtung der Laufzeit durch einen erwarteten Zinssatz in der Relation zu der Entwicklung des bestmöglichen Wertes. Ist es nicht möglich einen zukünftigen Zinssatz abschätzen zu können, kann die Konvexität ohne direkten Zusammenhang zur Duration betrachtet werden. Der Fokus der Betrachtung liegt deshalb auf Anleihen im hochkonvexen Bereich, welche eine Rendite erwarten ohne hierbei genauer auf die sinkenden oder steigenden Zinssätze einzugehen.

Eine Platzierung auf der Kurve des Zinssatzes ohne Beachtung der Duration charakterisiert sich hierdurch, dass die Chancen beziehungsweise Risiken eines Kursgewinns oder -verlustes der Anlagen bezüglich der Zinskurve dem marktrelevanten Index gleichen. Das betreffende Portfolio zeigt im Rahmen der restlichen Laufzeit eine entsprechende Sensitivität des Kurses wie jene eines marktrelevanten Portfolios des Indizes. Durch die Steigerung der Konvexität dieses Portfolios ist es möglich die Kontur zu ändern, ohne hierbei die Sensitivität des Kurses verändern zu müssen. Durch eine entsprechende Strategie ist es deshalb möglich, Anleihen mit unterschiedlichen Laufzeiten zu einem hochwertigen Portfolio zusammenzufügen. Eine konstante Duration kann somit durch die Kombination von Anleihen mit langer und kurzer Laufzeit erreicht werden, welche zusammen betrachtet eine Laufzeit mittlerer Länge ergeben. Aufgrund der Relation von der Konvexität und der restlichen Laufzeit ist das Ergänzen von Anleihen mit längerer Dauer von einem stärkeren Anstieg der Konvexität geprägt, als bei der Ergänzung von kurzfristigeren Anleihen.

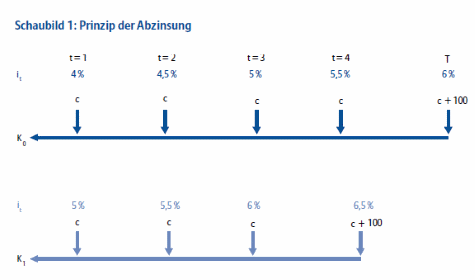
Die hochkonvexen Portfolios

Durch das Maximieren von Konvexität im Portfolio wird eine strategische Abschätzung auf die Marktbewegungen vorgenommen, welche einer Wette gleicht. Ein hochkonvexes Portfolio zielt darauf ab Änderungen des Zinssatzes zu erlangen, um von jenen profitieren zu können. Hierbei spielt die Richtung der Adjustierung des Zinssatzes keine Rolle. Erwarten eine Vielzahl an Teilnehmern des Marktes eine große und limitierte Schwankung des Preises, führt dies zu einer reduzierten Rendite. Als Grundsatz ist deshalb festzuhalten, dass Anleihen mit einer niedrigen Konvexität höhere Renditen verzeichnen als jene mit hoher Konvexität. Der Investor sollte deshalb bei einer Entscheidung für entweder ein hochkonvexes oder ein renditereiches Portfolio entscheiden. Bei minimalen Schwankungen von Renditen kann die hohe Konvexität die fehlende Rendite nicht zu jeder Zeit ausgleichen. Außerdem kann es bei einer riskanten Portfoliostruktur zu einer unerwünschten Platzierung auf der Zinskurve kommen. Bei der Platzierung auf einer Kurve sollte der Investor deshalb immer die entgangenen Erlöse beachten

Die Risiken eines hochkonvexen Portfolios

Die Betrachtung des Effekts der Konvexität verdeutlicht, dass eine proportionale Annäherung in Bezug auf die Rendite und den Preis zu einer Fehlschätzung führt, welche besonders bei höheren Renditeschwankungen deutlich wird. Die proportionale Annäherung der Preise in Relation zur Sensitivität zeigt den Versuch der Konvexität die Fehleinschätzung zu optimieren. In der Praxis ist jedoch das Verhältnis des Näherungs-Preises zweier Güter zueinander sowie deren Leistung maßgeblich. Bei der Analyse des marktrelevanten Indizes und dem Portfolio ist es demnach essenziell die gleichen Ansätze zu wählen, damit die Sensitivität des Zinses valide ausgeführt werden kann. Hierbei ist es nicht wichtig, ob die Konvexität als Hilfsmittel dieser Analyse genutzt wurde oder nicht. Der größte Risikofaktor ist somit von Änderungen des Niveaus des Marktzinses ausgehend. Im Vergleich hierzu ist die Renditesteigerung durch den Verkauf einer Anleihe, mit dem Ziel eine Anleihe mit einer größeren Rendite zu erwerben, klein, was in der Erhöhung der Konvexität begründet liegt. Das Risiko des Zinssatzes kann somit adjustiert werden, wenn die Duration alle Anlagegüter in Beziehung zur Duration eines Anlagegutes gesetzt wird und dieses mit dem marktrelevanten Index verglichen wird. Hierdurch kann der Fehler der Einschätzung im Rahmen der Adjustierung der Sensitivität eliminiert werden.

Zudem ist anzumerken, dass ein hochkonvexes Portfolio die Sensitivität des Preises immer auf den sofortigen Änderungen der Rendite bestimmen lässt. Bei einem größeren Anstieg der Rendite wird gezeigt, dass die Konvexität lediglich über einen gewissen Zeitraum betrachtet eine Relevanz für den Preis hat. Grundsätzlich kann somit gesagt werden, dass eine höhere Rendite mit einem größeren Risiko verknüpft ist. Die Erhöhung der Konvexität zeigt somit, dass diese meist bei einer hohen Sensitivität der Zinsen oder geringeren Erträgen genutzt wird. Bei einer Anleihe mit niedrigem nominalen Zinssatz und einer Notierung unterhalb des Rückzahlungskurses führt ein hochkonvexes Portfolio zu einem deutlich gesenkten Ertrag sowie der Steigerung der Duration. Auch das Risiko einer Änderung des Zinssatzes wird erhöht. Die Änderung der Struktur des Zinses ist somit maßgeblich für die gesamte Leistung der Anleihe. Deshalb ist es im Rahmen des Managements des Portfolios eher hintergründig die Konvexität als operative Maßnahme zu nutzen.